Question
Calculate the power output needed for a 950-kg car to climb a slope at a constant 30.0 m/s while encountering wind resistance and friction totaling 600 N. Explicitly show how you follow the steps in the Problem- Solving Strategies for Energy.
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 42 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
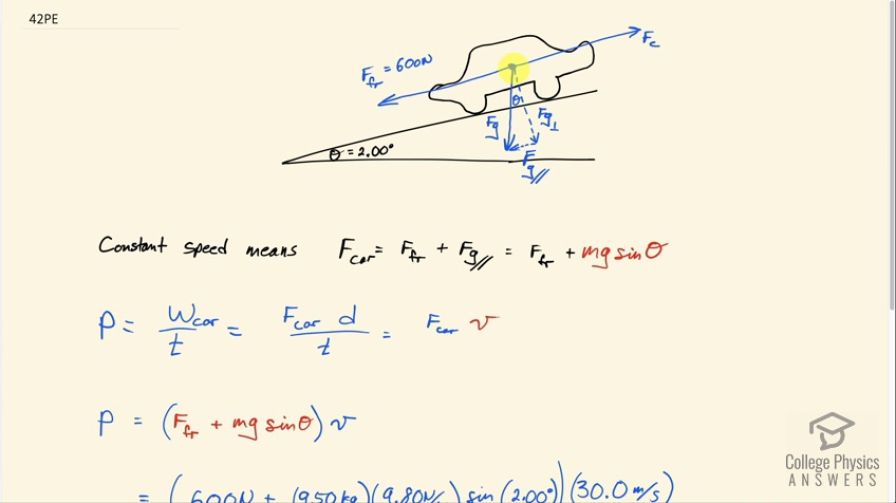
This is College Physics Answers with Shaun Dychko. This car is climbing a slope inclined at 2 degrees with a constant speed of 30 kilometers an hour and there's a headwind and some friction that totals 600 newtons and that is going to be opposing the direction of motion and the force applied by the car is gonna be in the direction of motion and there's also this gravity straight down which has some component parallel to the car's motion and this angle in here is Θ the same as the incline angle. So we want to know what the power output of the car has to be and so that's going to be the work done by the car divided by time and the work done by the car will be the force applied by the car multiplied by the distance it travels divided by time and we don't know what the distance travelled is but we do know what the rate of change in position is, the speed in other words. So this distance divided by time can be rewritten as v which is something that we are given in the question. And so what we need to figure out then is the force that the car applies. I mean the car is applying a force on the ground which in turn applies Newton's third-law counterpart back on the car but anyway that's a minor point. Okay! So the force that the car needs to exert multiplied by speed is what this question has become. So constant speed means that the force exerted by the car in to the right is going to equal the total of all the forces to the left where I'm defining, you know, right and left as being along this ramp. So the force to the left then is this friction which is 600 newtons that we are given plus this component of gravity that's parallel to the ramp and that's going to be gravity straight down which is mg multiplied by the sin of this angle Θ because we want to find this opposite leg of this triangle here and that's going to be found using sin Θ multiplied by the hypotenuse so it's mgsin Θ we can write in place of F g parallel. So we substitute all of this in for force of the car and multiply that by speed. So we have 600 newtons plus 950 kilograms times 9.80 newtons per kilogram times sin of 2.00 degrees and all that gets multiplied by 30.0 meters per second which is 27.7 kilowatts.
