Question
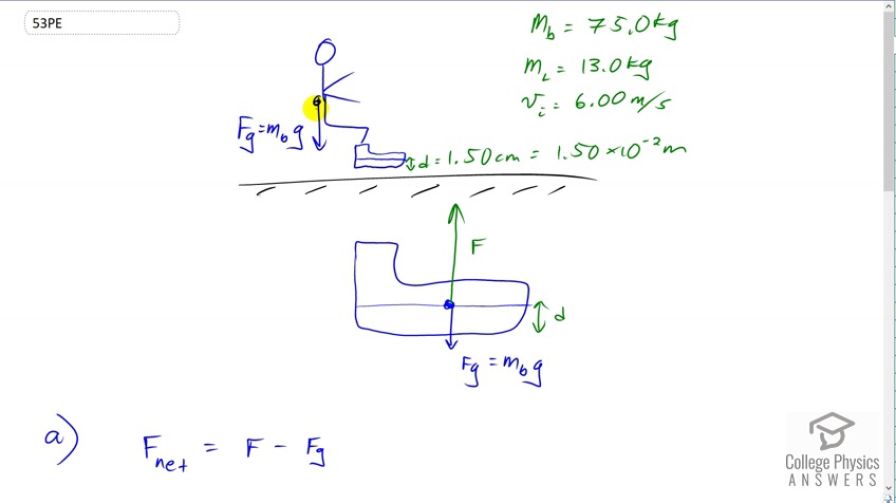
Jogging on hard surfaces with insufficiently padded shoes produces large forces in the feet and legs. (a) Calculate the magnitude of the force needed to stop the downward motion of a jogger’s leg, if his leg has a mass of 13.0 kg, a speed of 6.00 m/s, and stops in a distance of 1.50 cm. (Be certain to include the weight of the 75.0-kg jogger’s body.) (b) Compare this force with the weight of the jogger.
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 7, Problem 53 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This jogger with a body mass of 75 kilograms is running along and we assume that their body is not moving up and down. It's just their leg that's moving up and down. Their leg has a mass of 13 kilograms and it impacts the ground with an initial speed of six meters per second and then due to compression of the ground and the sole of their shoe, that compression is a total of 1.5 centimeters which is 1.5 times ten to minus two meters and in that distance the leg stops. So the leg loses some kinetic energy. So our job is to figure out what the force applied upwards on the foot is, and here's a zoomed in picture of the foot, and there is a force upwards that we're going to find there and there is gravity down. This is the total gravity on the entire body including the leg, so that's mass of the body times g. We can write our net force algebraically as net force is the force up minus the gravity force down and often we would write this equals mass times acceleration and while that's true, it's not useful for us here because we can't calculate the acceleration of their foot. The only thing we know is the distance over which it stops but we don't know how long it takes to stop. So we need to use a different method. We're going to use the work energy principle to figure out the net force in a second. But first, let's solve for F by adding F g to both sides and so the force upwards equals the net force plus gravity and that is net force plus the mass of the entire body times g. Now, we need to figure out the net force. So the work energy principle says that the net work done on the foot equals its change in kinetic energy. I suppose I should be saying foot and leg altogether, yeah. So, the net work is the net force multiplied by the distance over which the force is being applied and that's going to equal one half mass of the leg times its final speed which is zero, minus one half mass of the leg times its initial speed squared. So we get this, negative one half mass of the leg times initial speed squared is the change in kinetic energy and we divide this by d and that by d. We end up with the net force is the negative of mass of the leg times its initial speed squared divided by two times the distance over which it stops. So we substitute that in for F net up here so this gets substituted here in this line. So the force upwards is the negative of the mass of the leg times its initial speed squared divided by two times the distance over which it stops plus the mass of the body times gravitational field strength g, and now we can plug in numbers. So that's negative 13 kilograms times 6 meters per second squared divided by two times negative 1.5 centimeters. I put a negative there because the displacement of the leg is downwards here. Then plus 75 kilograms times 9.8 newtons per kilogram giving us 16,300 newtons is the force upwards on the foot and leg. So comparing that to the runner's weight we divided it by 75 times 9.8 and we get that the force applied upwards on their foot is greater than their weight by a factor of 22.2.
