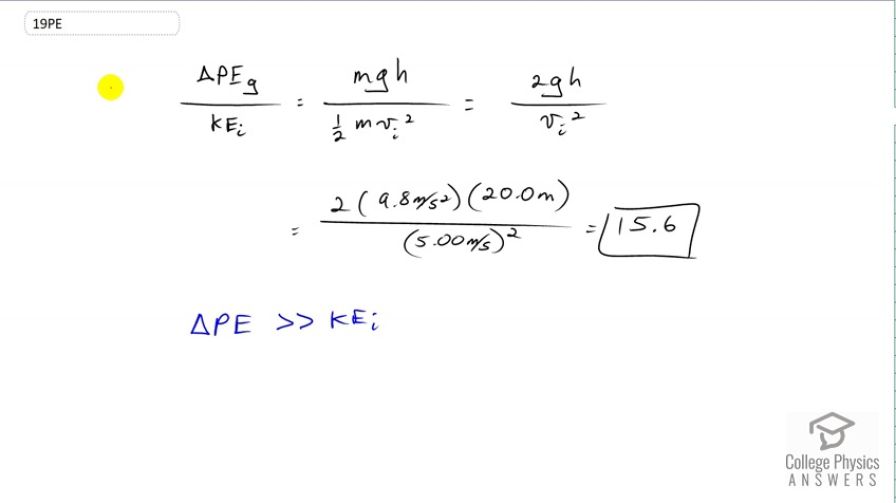
Question
In Example 7.7, we found that the speed of a roller coaster that had descended 20.0 m was only slightly greater when it had an initial speed of 5.00 m/s than when it started from rest. This implies that . Confirm this statement by taking the ratio of to . (Note that mass cancels.)
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 19 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We know from example 7.7 that when there is an initial kinetic energy for the roller coaster before it goes down the slope, it doesn't make that much difference which suggests that the change in potential energy as it goes down the slope is of much more significance than this small amount of initial kinetic energy because adding the initial kinetic energy to the potential energy change doesn't make much difference in the final kinetic energy. So we're going to confirm that delta PEg is much more than KE initial by dividing the two. So the change of potential energy of the roller coaster is its mass times g times the height over which it falls, and then we'll divide that by one half mass times the initial speed squared. The m's cancel and we can multiply top and bottom by two just to avoid having a fraction within a fraction which doesn't look very nice. So we have two gh on the top divided by the initial speed squared on the bottom. So that's two times 9.8 meters per second squared times 20 meters, divided by five meters per second squared, and that gives 15.6. So this confirms that the change in potential energy is much, much more than the initial kinetic energy. It's more than the initial kinetic energy by a factor of 15.6.
