Question
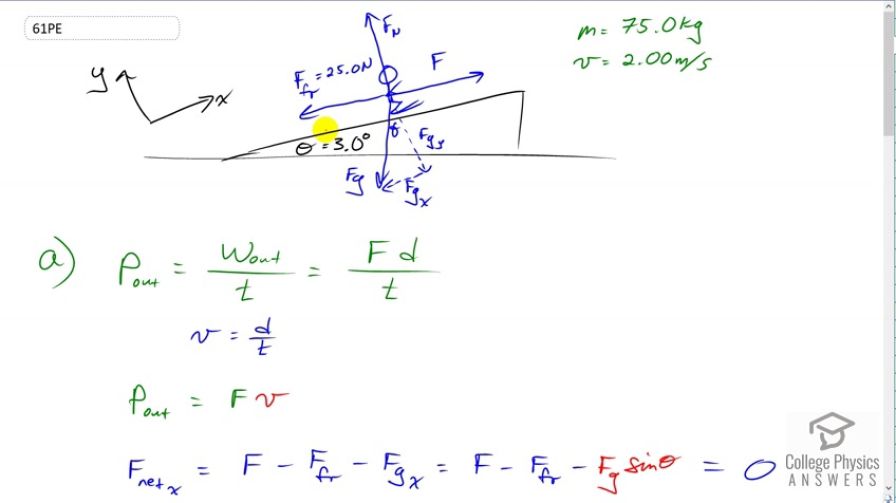
A 75.0-kg cross-country skier is climbing a slope at a constant speed of 2.00 m/s and encounters air resistance of 25.0 N. Find his power output for work done against the gravitational force and air resistance. (b) What average force does he exert backward on the snow to accomplish this? (c) If he continues to exert this force and to experience the same air resistance when he reaches a level area, how long will it take him to reach a velocity of 10.0 m/s?
Final Answer
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 7, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This skier is moving at constant speed of two meters per second up the slope. They have a mass of 75 kilograms and the slope is inclined at three degrees. So we're going to find the power output of the skier by dividing the work output divided by the time. The work output will be the force that the skier is, you know, exerting on the ground which in turn exerts that force on the skier. So this force in other words which I just labeled F multiplied by the distance over which the force is applied, divided by time. Now, we're not given distance nor time, but what we are given is the speed of the skier which is distance over time and so we can replace d over t with v. So, power becomes the force that they apply multiplied by the speed. So then the problem becomes how do we find the force? Well, in the x direction which is along the slope because I've tilted the coordinate system so that positive x is up along the slope, that net force in the x direction is the force that the skier applies forward minus the force of friction backwards which we're given as 25 newtons, and also minus the component of gravity which is in the negative x direction. That component of gravity F g x is the force of gravity multiplied by sine theta because in this triangle F g x is the opposite leg of the right triangle and this angle up in here is theta. Now, this x component of gravity is zero because they're moving at constant speed and so there is no acceleration. So, we can say F equals force of friction plus mg sine theta where I replaced F g with m g and I moved both of these terms to the right side by adding them to both sides. Then we can replace all of this in place of the force F in our power formula. So power output becomes force of friction plus mg sine theta, all times v. So that's 25 newtons plus 75 kilograms times 9.8 newtons per kilogram time sine of three, times two meters per second which gives 127 watts. Then to find the actual force in part B, well it's the force of friction plus the component of gravity in the x direction so that's 25 newtons plus 75 kilograms times 9.8 newtons per kilogram time sine of three, which gives 63.5 newtons. Then in part C, we're asked to figure out how long it would take to reach a velocity of ten meters per second if they applied the same force as they were going up the slope on a level surface. So in this case, the net force will be the force they applied to the right, minus the force of friction to the left. That's going to equal mass times acceleration and we'll divide both sides by m to get a equals the force they applied minus the force of friction divided by their mass. This is the acceleration we can plug into this formula which is that the final speed is the initial speed plus acceleration times time and we'll solve this for t by subtracting v i from both sides and then afterwards dividing both sides by a. We get time is the final speed minus the initial speed divided by acceleration and acceleration is this, so we'll multiply by its reciproca instead of dividing by it. So we've v f minus v i times m over F minus F r, so that's ten meters per second final speed, minus two meters per second initial speed, times 75 kilograms, divided by 63.467 newtons minus 25 newtons, which gives 15.6 seconds to reach ten meters per second.

