Question
Boxing gloves are padded to lessen the force of a blow. (a) Calculate the force exerted by a boxing glove on an opponent’s face, if the glove and face compress 7.50 cm during a blow in which the 7.00-kg arm and glove are brought to rest from an initial speed of 10.0 m/s. (b) Calculate the force exerted by an identical blow in the days when no gloves were used and the knuckles and face would compress only 2.00 cm. (c) Discuss the magnitude of the force with glove on. Does it seem high enough to cause damage even though it is lower than the force with no glove?
Final Answer
- The force with a glove is the weight of a 477 kg object. This is enough to do damage.
Solution video
OpenStax College Physics, Chapter 7, Problem 14 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
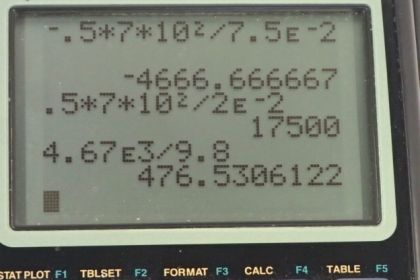
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A boxing glove hits a person's face and comes to a stop within 7.5 centimeters. The boxing glove and the boxer's arm has a combined mass of 7.00 kilograms and the initial speed of the glove is 10 meters per second. So we converted this distance into meters because we always need mks units in our questions—meters, kilograms and seconds. So we are gonna figure out the force exerted by the glove on this poor person's face. So the net work done is change in kinetic energy— that's the work-energy principle— and you could also say that the net work done is the net force multiplied by the displacement of course these being parallel as they are in this case. So that means we can say the force that we are trying to find times the distance is going to be the change in kinetic energy that is one-half mass times the final speed squared minus one-half mass times initial speed squared. The final speed is zero because the glove comes to a rest and so we have negative one-half mv i squared and we divide both sides by d to solve for the force. This negative sign indicates that the force on the glove is in the opposite direction to its displacement. So this is the glove and it's going this direction; the force on it is going to be in the opposite direction— as indicated by the negative sign— but the force on the poor person's face is gonna be in the opposite direction and will be positive because their displacement will be backwards to the right and so the force will be as well and so the force on the face will be the Newton's third law counterpart to this one, this being the force on the glove due to the face and this being the force on the face due to the glove— they have subscripts that are just switched around. Okay! So we find this force on the glove: negative 4.67 times 10 to the 3 newtons after we plug in numbers here and the force on the face then is the positive of that. Okay! Then in part (b) we say that suppose in the battle days of boxing when there were no gloves used, suppose the knuckles and fist come to a stop in only 2 centimeters instead of this padded greater distance of 7.50 centimeters. So we plug in the same numbers on top here so one-half times 7.00 kilograms times 10.0 meters per second and square that divided by this new 2 centimeter distance which we write as times 10 to the minus 2 meters and we get 1.75 times 10 to the 4 newtons which is almost 10 times greater than the force with the glove. Part (c) asks us to guess whether or not the force with the glove would be enough to cause damage to the person's face. In order to have a sense of what this number means, let's convert it into an equivalent mass that would have that weight. So F equals mg and so we rearranged to solve for m and it's the force divided by gravitational field strength. So we have 4.67 times 10 to the 3 newtons divided by 9.80 newtons per kilogram which is 477 kilograms. So the force applied by the glove in the first case here is the same as the weight on a mass with mass 477 kilograms and that is probably enough to do some damage.