Question
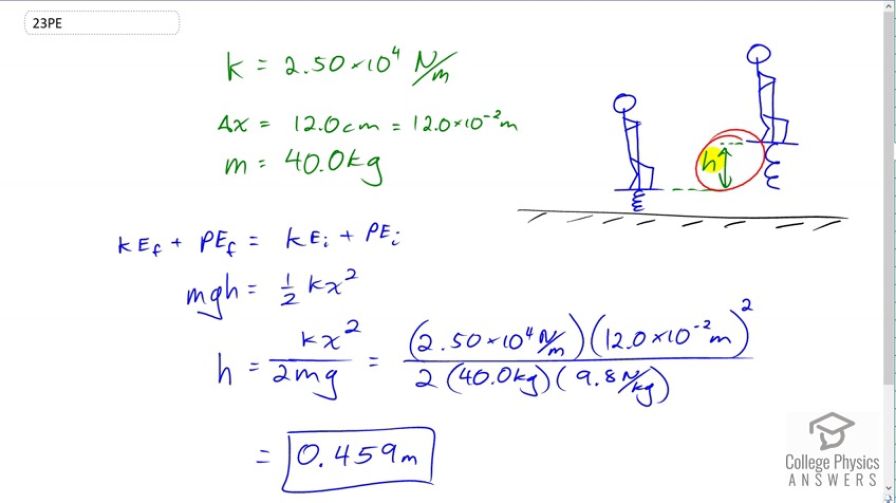
A pogo stick has a spring with a force constant of , which can be compressed 12.0 cm. To what maximum height can a child jump on the stick using only the energy in the spring, if the child and stick have a total mass of 40.0 kg? Explicitly show how you follow the steps in the Problem-Solving Strategies for Energy.
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This child is on a pogo stick and compresses the spring and then jumps up to some height h above the compressed spring level. Our job is to find this maximum height that's possible. So we're given some information that the spring constant is 2.5 times ten to the four newtons per meter. The spring is compressed by 12 centimeters which we convert into meters by going 12 times ten to the minus two meters and the mass of the stick and child is 40 kilograms. So the final total energy at this final time here when the child has leapt into the air equals the total mechanical energy at the beginning. There is no kinetic energy in either case because here the spring is completely compressed and the child is stationary so ke initial is zero and then at this position at the maximum height so they're not moving there either, so the final kinetic energy is also zero. The final potential energy is mgh and the initial potential energy is stored in the spring which is one half times spring constant times the amount by which the spring is compressed squared. We solve this for h by multiplying both sides by one over mg and we get h equals kx squared over two mg. So that's 2.5 times ten to the four newtons per meter times 12 times ten to the minus two meters squared, divided by two times 40 kilograms, times 9.8 newtons per kilogram, which is 0.459 meters. That is the height above this reference level which is the level at which the spring is fully compressed here.
