Question
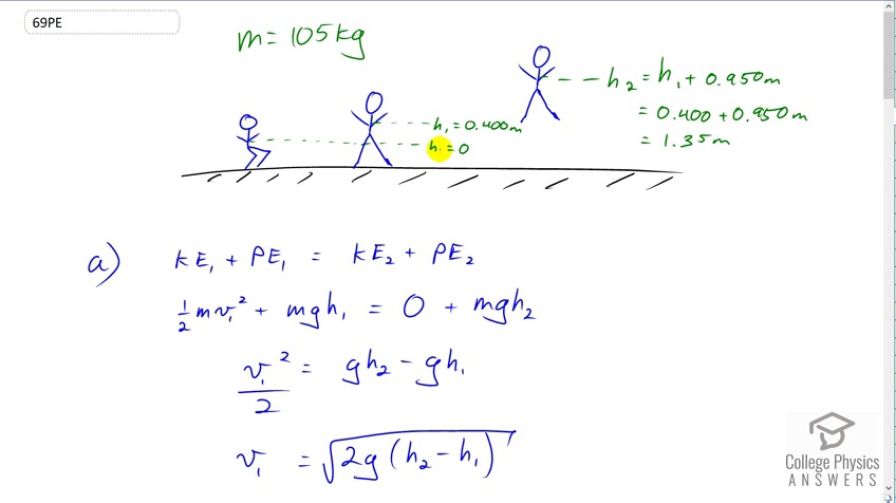
A 105-kg basketball player crouches down 0.400 m while waiting to jump. After exerting a force on the floor through this 0.400 m, his feet leave the floor and his center of gravity rises 0.950 m above its normal standing erect position. (a) Using energy considerations, calculate his velocity when he leaves the floor. (b) What average force did he exert on the floor? (Do not neglect the force to support his weight as well as that to accelerate him.) (c) What was his power output during the acceleration phase?
Final Answer
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 7, Problem 69 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This basketball player of mass 105 kilograms is crouched down and we'll call this crouched down position to be height zero. Then they exert a force and then when their legs are fully extended, they're at a height of 0.4 meters and we know that because we're told that they crouched down by 0.4 meters but we're going to call the crouched down to be our reference level zero so that when they're standing up we'll say that that's a height of 0.4. Then they leap into the air 0.95 meters above the standing upright position, so that means this 0.95 meters is above h one. So we have to add 0.4 meters to it to get the height above our reference level of the fully crouched down position. So the h two we're going to say is 1.35 meters. Now, in part A we're asked to figure out what will the speed of the basketball player be at this position which we label with the subscript one. So the kinetic energy at position one plus the potential energy at position one is going to equal the kinetic energy at position two, plus the potential energy at position two. But at position two they're at their maximum height and so there is no kinetic energy because they're not moving. So we have one half m v one squared, plus the m g h one equals zero plus m g h two. We will divide both sides by m so that the m's cancel and then subtract g h one from both sides and we get v one squared over two equals g h two minus g h one. We can factor out the g, multiply both sides by two and also take the square root of both sides to get this expression for the speed at position one. So that's the square root of two times 9.8 meters per second squared times 1.35 meters minus 0.4 meters which gives 4.32 meters per second. Then in part B, we're asked what is the force that the basketball player applies upwards in order to launch to this height here. Well, the total potential energy that they have at this position which is with respect to the crouched down position by the way, is given by the work done by the athlete. The work done by the athlete is the force that they apply which is what we’re trying to find, multiplied by the distance over which they apply it which is this distance here from the crouched down to the fully standing position. So they apply this force over the distance of each one. So we can solve this for the applied force by dividing both sides by h one. We get that the force that they apply is m g h two over h one. So it's 105 kilograms times 9.8 newtons per kilogram times 1.35 meters, divided by 0.4 meters which is 3470 newtons. Then we're asked in part C to find the power output of the athlete. So we have to take the work that they do, which is the applied force multiplied by the distance over which they apply the force, each one the same as this, you know we had this W a over there already, and we divide that by the time that they spend applying that force. Now the time is a bit tricky to figure out but we'll get there. We know that this distance h one from fully crouched to standing equals their initial speed times time which is zero because the initial speed is zero when they crouch down, plus one half times acceleration times time squared. This is useful because we can figure out what acceleration is because we know what their force is that they apply and we know their mass. So, we can solve this for t by multiplying both sides by two over a, and then switch the sides around and then take the square root of both sides. So t is the square root of two h one over a. Now, we next turn to a different color of ink. We have black now because it's a new train of thought where we're trying to figure out the acceleration. So the net force equals mass times acceleration, that's Newton's Second Law, and the net force is F a upwards minus m g downwards. So we made that substitution here and then we solve for a by dividing both sides by m and switching the sides around. So it's the applied force minus m g over m. Now we have an expression for applied force already from part B. The force due to the athlete is m g h two over h one so we'll substitute that here, m g h two over h one for F a and then the m's cancel. Then we can factor out the common factor g and we get the acceleration is g times h two over h one minus one. That we can substitute in for a in our formula for time, and so we have t equals square root two h one over g h two over h one minus one. Then that in turn we can substitute for t in our expression for power. Now instead of dividing by this fraction, I'm going to multiply by its reciprocal just to keep things a bit neater because I don't like dividing fractions by fractions. So the power output is F a h one multiply by the square root of g h two over h one minus one over -- let's not forget the number two there which I forgot before. So when we take this F a h one divided by time, we're multiplying by its reciprocal and so we're multiplying by g h two over h one minus one, all over two h one. Okay. Then we can substitute the expression for -- I mean at this point we can actually plug in numbers if we wanted to. I just feel like doing some algebra for fun basically. So we have the expressions for the force due to the athlete is m g h two over h one from part B, there, and the h ones cancel. So we're left with m g h two times square root g h two over h one minus one, all over two h one and then we can plug in numbers. Notice that by doing things this way we have not used any calculated number from previous work. So we haven't used the speed of part A and we haven't used the force from part B, and so this increases our chance of getting a correct answer because we're not using any calculated number that we've done because maybe we made a mistake in one of those numbers. So this uses numbers that are just from the question. 105 kilograms times 9.8 meters per second squared times 1.35 meters, times square root of 9.8, times 1.35 over 0.4 minus one, divided by two times 0.4 meters gives 7.49 kilowatts of power from the athlete.


