Question
(a) What is the available energy content, in joules, of a battery that operates a 2.00-W electric clock for 18 months? (b) How long can a battery that can supply run a pocket calculator that consumes energy at the rate of ?
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 40 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
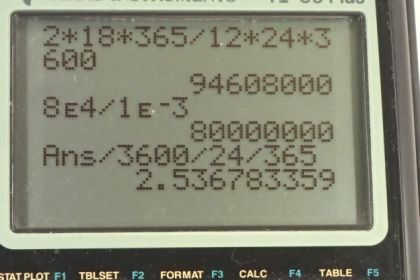
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The power that the battery has is the work that it does divided by time and the work that it does is the energy that it uses and we can solve for that by multiplying both sides by t. So the energy in the battery then is its power multiplied by its time. So it's running a 2.00 watt clock and it's running for a period of 18 months and then we have to convert this into seconds so we'll convert months into days by multiplying by 365 days for every 12 months times 24 hours per day times 3600 seconds per hour and we are left with seconds and this works out to 94.6 megajoules of energy in the battery. In part (b), we are asked how long will a pocket calculator operate given a certain energy in the battery and power consumption by the calculator. So we'll solve this for t by multiplying both sides by t over P and we are left with time is the energy in the battery divided by the rate of energy use of the calculator. So that's 8.00 times 10 to the 4 joules divided by 1.00 times 10 to the minus 3 watts and this works out to 8.00 times 10 to the 7 seconds which is a kind of a hard number to conceptualize so let's convert this into years. And so we'll multiply by 1 hour for every 3600 seconds times 1 day for every 24 hours times 1 year for every 365 days and we are left with 2.54 years.