Mountain climbers carry bottled oxygen when at very high altitudes. (a) Assuming that a mountain climber uses oxygen at twice the rate for climbing 116 stairs per minute (because of low air temperature and winds), calculate how many liters of oxygen a climber would need for 10.0 h of climbing. (These are liters at sea level.) Note that only 40% of the inhaled oxygen is utilized; the rest is exhaled. (b) How much useful work does the climber do if he and his equipment have a mass of 90.0 kg and he gains 1000 m of altitude? (c) What is his efficiency for the 10.0-h climb?

Video Transcript

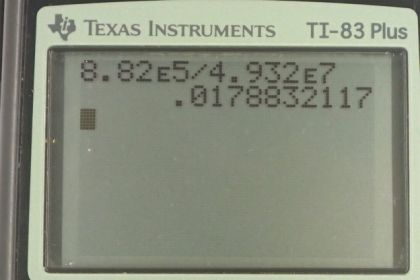
This is College Physics Answers with Shaun Dychko. In part A of this question we're going to calculate the volume of oxygen the climber utilizes and Table 7.5 says that when climbing stairs a person utilizes 1.96 liters of oxygen per minute. In this case, climbing the mountain they're using twice as much oxygen per minute and we're told there is a ratio of 40 percent is the amount of oxygen utilized by the body versus the amount of oxygen inhaled or consumed which means one liter is consumed for every 0.4 liters utilized. So these oxygens utilized cancel and we're now given the amount of oxygen consumed. Then we multiply that by ten hours times 60 minutes per hour and now the minutes cancel there and the hours cancel there and we'll be left with the amount of oxygen consumed. So it's 1.96 times two, divided by 0.4 times ten times 60, gives 5.88 times ten to the three liters of oxygen consumed. The work output of the climber is equal to the force of gravity multiplied by the height of the climb. So that's 90 kilograms times 9.8 newtons per kilogram, times 1000 meters which is 8.82 times ten to the five joules. Their efficiency is the useful work output divided by the energy input and the energy input is going to be 685 watts which is the energy consumed while climbing stairs in Table 7.5. Then we multiply that by two as we're told in this question because there is low air temperature and there is wind blocking them and so on, o they use twice as much energy as somebody just climbing stairs, times by ten hours times 3600 seconds per hour gives us 4.932 times ten to the seven joules. So we take the work output divided by the work input which gives about an efficiency of 1.79 percent.