Question
A shopper pushes a grocery cart 20.0 m at constant speed on level ground, against a 35.0 N frictional force. He pushes in a direction below the horizontal. (a) What is the work done on the cart by friction? (b) What is the work done on the cart by the gravitational force? (c) What is the work done on the cart by the shopper? (d) Find the force the shopper exerts, using energy considerations. (e) What is the total work done on the cart?
Final Answer
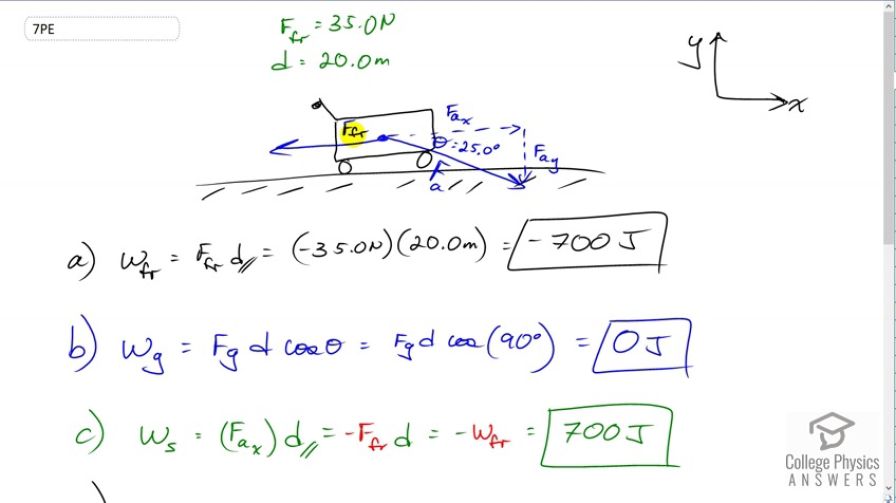
a)
b)
c)
d)
e)
Solution video
OpenStax College Physics, Chapter 7, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a shopping cart being pushed to the right in the positive x direction. There is a friction force going to the left of 35 newtons and the cart is going to be pushed to the right 20 meters and the shopper is applying a force Fa at an angle of 25 degrees below the horizontal. So there is a component of an applied force in the x direction and a component that is vertical. In part A we're asked to find the work done by the friction force and so that is the friction force multiplied by the the component displacement parallel to the friction although we don't have to worry about that parallel business the displacement and friction are anti-parallel to be precise because they are in opposite directions. So that means we have to put a negative for the friction because it's in the negative direction to the left and then the displacement is to the right, 20 meters, multiply those two together and you get 700 joules negative is the work done by friction. The work done by gravity is the force due to gravity multiplied by the component of the displacement parallel to the gravity. This theta here is a bit confusing though because it's not the same theta as there. This angle, let's give it a different name. This angle is meant to be the angle between the gravity force and the displacement. So the gravity force which I haven't actually labeled here is downwards. The displacement is to the right and so the angle between them is -- we'll call it gamma say -- it is 90 degrees. So the cosine of 90 is zero and that means we don't have to do anymore calculating because whatever these things are, multiplied by zero it's going to give zero joules for the work done by gravity. Okay. So that happened because there is no component of the displacement in the direction of gravity. Then the work done by the shopper is going to be the component of the force they apply which is parallel to the displacement, multiplied by the displacement. Now this Fa x is of equal magnitude to the friction force. We know that because the shopping cart is moving at constant speed. So we substitute negative friction force in place of Fa x. This friction force multiplied by displacement, this part here, is the work done by friction and so we have a negative in front of that. So negative of negative 700 is positive 700 joules. Then we're asked to find what is the force applied by the shopper and use energy considerations to find it. So we'll say that Fa x multiplied by the displacement is the work done by the shopper, and the x component of the applied force is the applied force multiplied by cosine of theta because this adjacent leg, you have to find it by multiplying the hypotenuse by the cosine of the angle, then substitute that in for Fa x and we have Fa times cos theta times displacement equals the work done by the shopper. Then divide both sides by cos theta d and you get the applied force is the work done by the shopper divided by d times cos theta. So that's 700 joules divided by 20 meters times cosine of 25 which gives 38.6 newtons. We expected some number that is bigger than the friction force because there is a component that is downwards in addition to the component that already equals friction horizontally, and so added to that is this component downwards so we expected some number greater than 35. Doing the reality check on your answers is always a good idea to see if they make sense. Part E asks to find the net work and that is the net force multiplied by displacement but there is no net force because this cart is moving at constant speed and so the net work done is zero joules.
