Question
A car advertisement claims that its 900-kg car accelerated from rest to 30.0 m/s and drove 100 km, gaining 3.00 km in altitude, on 1.0 gal of gasoline. The average force of friction including air resistance was 700 N. Assume all values are known to three significant figures. (a) Calculate the car’s efficiency. (b) What is unreasonable about the result? (c) Which premise is unreasonable, or which premises are inconsistent?
Final Answer
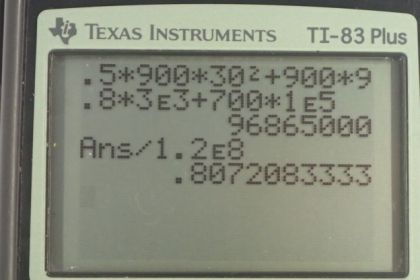
a) 81%
b) This efficiency is unreasonably high. Table 7.2 shows a typical gasoline engine efficiency is ~30%. The maximum theoretical efficiency is ~50%. See an explanation of the Otto cycle from MIT.
c) 1.0 gal of gasoline is inconsistent with 100 km traveled, especially up a steep hill gaining 3.0 km in altitude.
Solution video
OpenStax College Physics, Chapter 7, Problem 65 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to calculate the efficiency of this car and let's begin by writing down all the information we're given. We're told that the car has a mass of 900 kilograms. It reaches a final speed of 30 meters per second starting at rest. It travels a distance of 100 kilometers which is one times ten to the five meters. It gains an altitude of three kilometers which is three thousand meters and the energy consumed by the car is the energy in one gallon of gasoline, and looking at Table 7.1 we can see that there are 1.2 times ten to the eight joules per gallon. That means the car consumes 1.2 times ten to the eight joules of energy. The force of friction opposing its motion is 700 newtons. Now to calculate the efficiency we need to find the energy output and divide that by the energy consumed. So the energy input we've already got here, it's 1.2 times ten to the eight joules and the energy output we'll have to do some work to calculate it. Energy output will equal the kinetic energy imparted to the car as well as its increase in gravitational potential energy as it goes up this height three kilometers, and also need to offset the energy lost due to friction which will be the friction force applied over some distance like 100 kilometers. So the change in kinetic energy is one half m v f squared because you know, normally I would write one half m v f squared minus one half m v i squared but there is no initial velocity here, it's zero. So the change in kinetic energy is just this, and then we have the change of potential energy is the mass times gravitational field strength times the change in height. Then friction is, force of friction times distance and now we plug in numbers. We have one half times 900 kilograms times 30 meters per second final speed squared, plus 900 kilograms times 9.8 times three times ten to the three meters of height gained, plus 700 newtons friction force times the distance traveled of one times ten to the five meters, giving 9.6865 times ten to the seven joules of energy output. So the motor needs to provide this much energy in these three forms. So the energy output divided by the energy input is our efficiency and this works out to 81 percent which is not realistic. Table 7.2 shows a typical gasoline engine efficiency is about 30 percent and the maximum theoretical efficiency is about 50 percent. A perfect engine with no friction and no problems of any kind will at most achieve efficiency of about 50 %. You'll read about calculating these theoretical efficiencies in the thermodynamics chapter. Carnot efficiency is one type of theoretical maximum efficiency. I think gasoline engines use something called the autocycle. I'll try to provide some links in the final answer there about those topics. So part C I would say that one gallon of gasoline consumed is inconsistent with the 100 kilometers traveled so either the distance traveled is actually less than 100 kilometers or the amount of gasoline consumed is more than one gallon. This is especially true, given that the car is going uphill. We would expect the mileage of the car to be even less than typical, given that it's going uphill.