Question
A 500-kg dragster accelerates from rest to a final speed of 110 m/s in 400 m (about a quarter of a mile) and encounters an average frictional force of 1200 N. What is its average power output in watts and horsepower if this takes 7.30 s?
Final Answer
, or
Solution video
OpenStax College Physics, Chapter 7, Problem 37 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
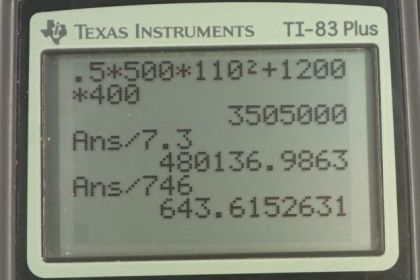
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The net work done on the dragster is equal to its change in kinetic energy. There are two forces doing work on the dragster. One is the force applied you know, by the ground on to the dragster. Well, let's call this the force due to the dragster accelerating it forwards in the direction of motion. There is also the force of friction opposing the motion going to the left. There's also gravity and normal force but we don't care about those because they don't do any work since their direction is perpendicular to the displacement. So the net work done is the work done by the dragster plus the work done by the force of friction. The work done by the force of friction is the force of friction multiplied by the displacement. But I've put this negative sign here to illustrate that the force of friction is in the negative x direction. So we're defining to the right being positive here. So we substitute that in place of the work done by friction here, where at this point I have subtracted the work done by friction from both sides to solve for the work done by the dragster because we need to figure out the work done by the dragster and then divide that by time in order to find the power output of the dragster. So, here we are at this point. We have a minus the work done by friction and then there is a negative contained within that work done by friction term, and negative and negative makes a positive. So the work done by the dragster is the change in kinetic energy plus the force of friction times the displacement. The change in kinetic energy is one half m v final squared minus one half m v initial squared but there is no initial speed because it starts from rest and so this reduces to one half m vf squared plus force of friction times displacement. So that's one half times 500 kilograms times 110 meters per second final speed squared, plus 1200 newtons friction force, times 400 meters displacement which is about a quarter mile. That gives 3.505 times ten to the six joules. So then we take that energy output and divide that by the 7.3 seconds that it takes to do that which is 480 kilowatts. Then write that in watts and keep some more digits since this is an intermediate calculation as we convert this into horsepower by multiplying by one horsepower for every 746 watts which gives a horsepower of 644 horsepower.