Question
A woodpecker's brain is specially protected from large decelerations by tendon-like attachments inside the skull. While pecking on a tree, the woodpecker's head comes to a stop from an initial velocity of 0.600 m/s in a distance of only 2.00 mm. (a) Find the acceleration in and in multiples of (). (b) Calculate the stopping time. (c) The tendons cradling the brain stretch, making its stopping distance 4.50 mm (greater than the head and, hence, less deceleration of the brain). What is the brain's deceleration, expressed in multiples of ?
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 32 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
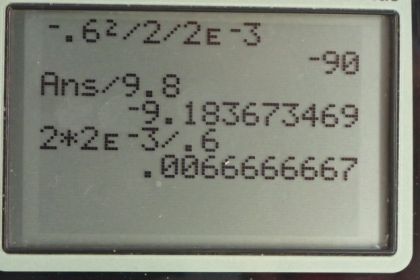
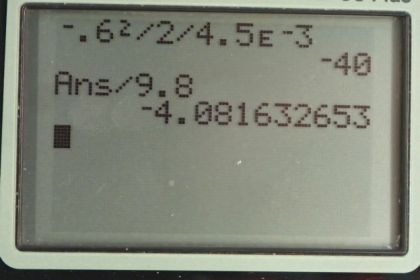
This is College Physics Answers with Shaun Dychko. A woodpecker's head has an initial velocity of 0.600 meters per second as it's going towards the tree and then it stops when it strikes the tree and it stops at a distance of 2 millimeters and when you are writing down the data that you know, it's usually a good idea to take care of any unit conversion issues that might come up. So this is expressed in millimeters and we always, almost always, want mks units— meters, kilograms and seconds— and so this should be converted into meters and the prefix 'milli' means times 10 to the minus 3 and the initial position we assume is zero. So part (a) asks us to find the acceleration and we choose equation [54] because it has all the things that we know plus the one thing that we don't know. So the first thing I'm going to do is replace all the variables that have the value zero to simplify our equation before we do any algebra to solve for a. So the final velocity is 0 so that's why this 0 is here and the initial position is 0 and so that's why x naught does not appear on this line. So I have rewritten this with the 0's substituted so we have 0 equals initial velocity squared plus 2 times acceleration times final position and then we solve this for a and we subtract v naught squared from both sides and then afterwards, we divide both sides by 2x and switch the sides around and we end up with this line here; acceleration is negative v naught squared over 2 times final position. So that's negative of 0.600 meters per second—initial velocity—squared divided by 2 times 2 millimeters written as 2 times 10 to the minus 3 meters giving negative 90.0 meters per second squared is the acceleration of the woodpecker's head. And expressed in terms of g's which is acceleration due to gravity, we multiply this negative 90 meters per second squared by 1 g for every 9.8 meters per seconds squared and the meters per second squared units cancel leaving us with g's, that is negative 9.18 g's. And part (b) asks us to figure out how much time it takes for the woodpecker's head to stop. So we choose equation [50] because it contains things that we know and it contains raw data in it. So what I mean by that is we don't want to choose an equation that has an acceleration term in it because there's a possibility that we have made a mistake in our acceleration calculation so we always choose formulas, where possible, that have things that are given to us in the question. So we replace this average velocity with this formula [51] and combining the two, we have final position is initial position plus initial velocity plus final velocity divided by 2 multiplied by time and then we replace all the terms that are zero. So the initial position is zero and the final velocity is zero and we are left with final position is initial velocity multiplied by time divided by 2 and this we can solve for t by multiplying both sides by 2 over v naught and then switch the sides around. So we have time is 2 times final position divided by initial velocity. So that's 2 times 2 millimeters written as 2 times 10 to the minus 3 meters divided by 0.600 meters per second giving 6.67 milliseconds. And then part (c) now the tendons that are attached to the brain inside the woodpecker's skull cause the brain to go further than the head does when the head stops and this is useful because it increases the stopping distance and by doing so decreases the acceleration because the acceleration is inversely proportional to this distance over which the brain is decelerating. So we have this same formula that I just copied from up here; negative v naught squared over 2x. and we have substituted in 4.5 times 10 to the minus 3 meters instead of 2 times 10 to the minus 3 meters and this gives an answer of negative 40 meters per second squared or in terms of g's, negative 4.08 g's and so by increasing the stopping distance by a little bit more than 2 times, we have decreased the acceleration by at least a factor of 2.