Question
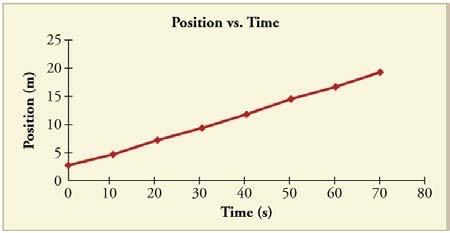
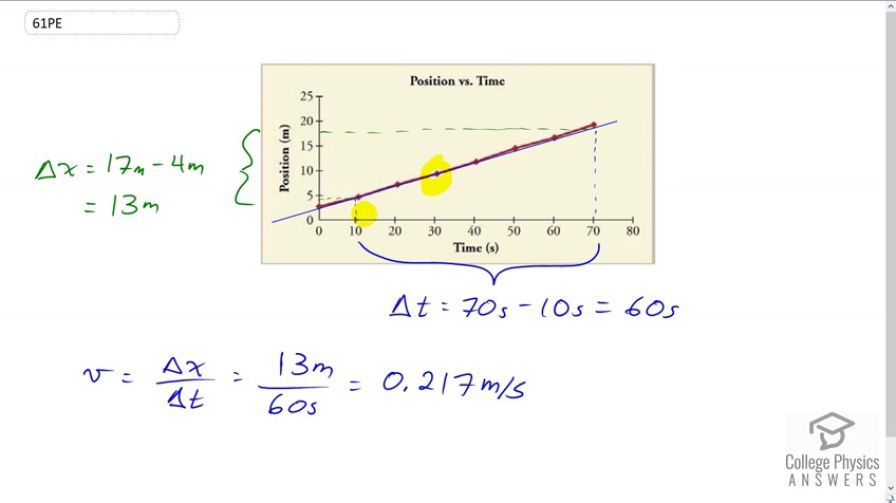
Using approximate values, calculate the slope of the curve in Figure 2.62 to verify that the velocity at is 0.24 m/s.
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. To find the instantaneous velocity at 30 seconds, we need to take a tangent line to the curve at this point. So the tangent line will touch the curve only at this point and not at any other point, although it's hard to really see that because this red line is nearly a straight line. But I've drawn a blue line here as my tangent line. So then we find the slope of the tangent by finding out how much it rises, and that's a change in position of about 17 meters at the top minus 4 meters at the bottom. Then we're going to divide that rise by the time interval over which this change of position occurs. So it starts at about 10 seconds up to about 70 seconds and so that's a time interval of 10 minus 70, 70 minus 10 which is 60 seconds. So we have the velocity then is 13 meters divided by 60 seconds which is 0.217 meters per second which is close enough to 0.238 meters per second that we were meant to verify. We don't expect to get exactly that number because we're doing an approximation here visually using a graph. So, close enough though.
Comments
How do we get the tangent line?
I think I would be wise to draw a circle, it is not efficient and accurate if doing it by hand, pretty useless in fact unless you want a close estimate. So usually I use demos to make a circle around the point and then you just have to know some basic trigonometry which includes the unit circle, radians, tan sin and cos and it becomes easy. Tan is the slope of the line, you can measure the degrees of the point and then convert it to radians, then you can find sin and cos which you will also learn about in two dimensional kinematics, it is the basis of kinematics and even dynamics.

