Question
Dragsters can actually reach a top speed of 145 m/s in only 4.45 s—considerably less time than given in the textbook examples. (a) Calculate the average acceleration for such a dragster. (b) Find the final velocity of this dragster starting from rest and accelerating at the rate found in (a) for 402 m (a quarter mile) without using any information on time. (c) Why is the final velocity greater than that used to find the average acceleration? Hint: Consider whether the assumption of constant acceleration is valid for a dragster. If not, discuss whether the acceleration would be greater at the beginning or end of the run and what effect that would have on the final velocity.
Final Answer
a)
b)
c) see video for discussion.
Solution video
OpenStax College Physics, Chapter 2, Problem 37 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
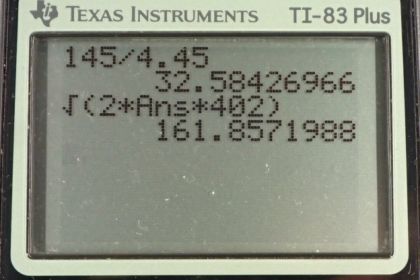
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko The dragster starts from 0 meters per second and reaches a final speed of 145 meters per second when he crosses the finish line and it takes 4.45 seconds to do that. So, part A asks us to figure out what is the acceleration of the dragster on average over the entire trip. So, we have final velocity equals initial velocity plus acceleration times time and we're going to solve this for a. So, we'll subtract v naught from both sides and then switch the sides around. And we have at equals v minus v naught. And then, divide both sides by t. And now, we have acceleration as final velocity minus initial divided by time. So, it's 145 meters per second minus 0 divided by 4.45 seconds which is 32.6 meters per second squared acceleration. Now for part B, we're told to use this number. And calculate what the final velocity is that you would expect given this acceleration and a quarter mile or 402 meters. So... we are told... Don't use any information about time. And so, this is why we have to use this calculated number in our part B. Normally, we would not use a number that we calculated in order to be cautious by avoiding, you know, using a number that might have a mistake in it, but in this question, it tells us we have to. So, we will go ahead with that. We have final velocity squared equals initial velocity squared plus 2 times acceleration times the displacement and because it starts from rest, that means initial velocity is 0, in which case this equation reduces to just 2a times x minus x naught. And then, we take the square root of both sides and we have final velocity equals square root of 2 times acceleration times x minus x naught. Now, technically, this could be plus or minus, but we can use the physics of the situation to know that the final velocity will be in the same direction as the acceleration and we can take that direction to be positive. And so, we can take the positive square root. And so, that is square root of 2 times 32.584 meters per second squared times 402 meters, noticing that I've used a unrounded number here for the acceleration. Looking at my calculator, I have more digits in this value. And so, we use as many as we can in order to avoid intermediate rounding error. So, that works out to 162 meters per second. Now, this final velocity that we calculated assuming this acceleration of 32.6 is greater than the final velocity that is actually measured of a 145. And... And the reason for that is that this acceleration is an average and the dragster does not have this acceleration at all times. This calculation assumes that the acceleration is exactly this all the time, but in reality, that's not true. And at the very beginning, there is no air drag. The dragster is not moving. And so, and also first gear is really high torque. And so, those are two reasons why the acceleration will be really high at the beginning of its trip. But then, as the dragster picks up speed and begins using higher gears which have less torque combined with the air resistance which is very significant when you get to high speeds. That means the acceleration will be probably quite a bit less than this during the last part of its trip. And so, it won't have this acceleration all the time. And... And so, its final velocity will be less than what you would assume given that constant acceleration which doesn't actually happen.