Question
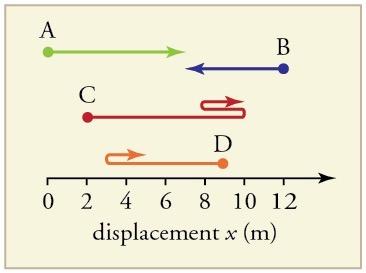
Find the following for path B in Figure 2.59: (a) The distance traveled. (b) The magnitude of the displacement from start to finish. (c) The displacement from start to finish.
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 2 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to find the distance traveled for part (a) along this path labeled B so this blue path starting at about 12 here to a final position I'd say of about 7 meters on this x-axis. So going from 12 to 7 in a straight-line, is a distance of 5 meters, that's 12 minus 7. Now part (b) asks us to find the magnitude of the displacement but I prefer instead to figure out what that displacement is in part (c) and then go back to part (b) to find its magnitude. So displacement is the change in the exposition and that is the final exposition minus the initial exposition and the final exposition is positive 7— it's positive because it's to the right of zero here. So that's positive 7 minus the initial exposition which is positive 12 and 7 minus 12 makes negative 5 and this negative sign has to be part of your answer when you are asked to figure out what is displacement; displacement is a vector and this negative or positive indicates the direction of that vector so the displacement is negative 5 meters. Now for part (b), we can find the magnitude of that which is to say just take this number and make it positive if it's negative and if it was positive 5 meters displacement, well, the magnitude would be the same. So it's the size of this number is the magnitude and that is 5 meters and the magnitude of the displacement is the same as the distance in this case because there's no back and forth motion; if there was some back and forth then the distance would be increasing as one goes back and forth but the displacement would not be and in that case, magnitude of displacement and the distance would not be the same for path C and path D but for path B because it is a single straight-line, the displacement magnitude is the same as the distance.