Question
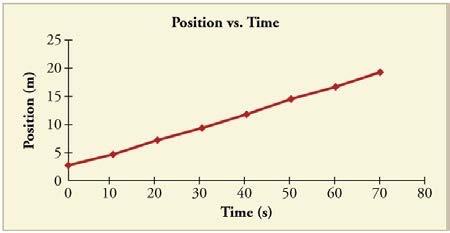
Using approximate values, calculate the slope of the curve in Figure 2.62 to verify that the velocity at t = 10.0 s is 0.208 m/s. Assume all values are known to 3 significant figures.
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 60 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. To find the velocity, we need to take the tangent at the time of 10 seconds. This will give us the velocity at 10 seconds— the instantaneous velocity it's called because it's the velocity at that particular instant of 10 seconds— and then we find the slope of this tangent line which is in blue and we'll find the rise over run of this line. So I have chosen at 40 seconds to figure out what is the position of this tangent line. And this green line it doesn't go to the red line, it goes all the way to the green line because you have to use the tangent line here; we don't know wanna use the red line because the red line is just the line connecting the dots of our position-time graph. So we wanna find the change in position divided by the change in time and so that is about 10.5 meters is where the y-coordinate of this point on the tangent line is and the corresponding time is 40 seconds and from that 10.5 meters, we subtract our initial position which is about 2 meters say, and then that's that; 0 seconds is when the position is 2 meters. So we take the change in position for this tangent line and divide by the time interval between those positions and we get 0.21 meters per second is the velocity at 10 seconds.
