Question
Figure 2.68 shows the displacement graph for a particle for 5 s. Draw the corresponding velocity and acceleration graphs.
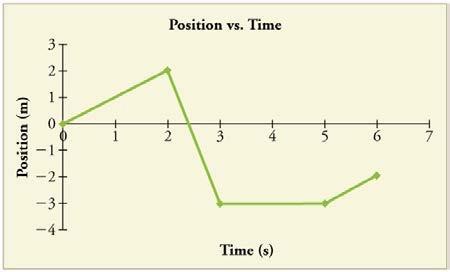
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 2, Problem 66 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. A particle is traveling for 5 seconds and here is its position versus time and we have to figure out what the velocity-time graph is and the acceleration-time graph. So it's traveling at a constant speed or constant velocity from 0 to 2 seconds and you can tell that because this position-time graph is a straight-line and so between 0 and 2 seconds, we can say that the velocity is 1 meters per second because we found the change in position and we could consider, you know, this time here to be the final position and the position at this time initially that's 2 meters minus 0 meters divided by the time difference which is 2 seconds to 0 seconds. So this makes 1 meters per second. and this is a constant velocity all the way until 2 seconds and so that's why I have written 1 meters per second at 2 seconds as well. But the strange thing about this graph is that it is discontinuous and what that means is there's no gentle curve at certain points; at this point here, there's an abrupt change in direction all of a sudden and that's a non-physical thing because you can't just instantly change positions and so this is going to cause some problems in our acceleration graph because at 2 seconds, we can also say that the velocity is negative 5 meters per second and you have this bizarre circumstance where you have two different velocities at the same time and you can't really distinguish between one or the other here because you can't there's no way to see how the velocity is changing through this time here; it seems to be changing instantly. So it's a weird graph for sure. And now to calculate this second velocity, we find this final time here of 3 seconds and this initial time at 2 seconds and we have a change in position of final position of negative 3 and an initial position of 2 and so we take the difference in position divided by the difference in time and this makes negative 5 meters per second. And at 3 seconds, we instantly get a velocity of zero. I could have also have written 3 seconds velocity negative 5 meters per second because it is right up until 3 seconds and then at 3 seconds, it instantly changes to 0 and it continues along at 0 until 5 seconds at which point, it changes its slope to 1 meters per second and we found that by taking this final position negative 2 and then minus the initial position of negative 3 which makes positive 1 in the numerator and divide by 6 seconds minus 5 seconds. Okay. So we can graph this now and we'll have 1 meters per second at 0 seconds and that will go all the way up until 2 seconds and then at 2 seconds, we immediately change to negative 5; I suppose I could draw a line vertically down like this. Now in math class, a line vertically down like this would suggest that this graph is not a function because a function means that you only get one y-coordinate for every x-coordinate and because it's not a function, in physics class, you can say it is non-physical— this is not something that can happen in reality— you can't have multiple different velocities all at a single time. Okay. But this is the best we can do given the information we have here so we'll draw it out that way anyway. And then we can carry on at negative 5 meters per second velocity until we get to 3 seconds so we don't have to go that far so until 3 seconds and then at 3 seconds, we are gonna change to 0 immediately and so we are gonna carry along the time axis here until we get to 5 seconds at which point we immediately jump back up to 1 meters per second until 6 seconds. So that's the velocity-time graph; that's kind of a step-wise function although it's not a function technically because of these multiple velocities all at a single time, okay. Now more bizarreness will happen in this acceleration graph because when we change from 1 meters per second to negative 5 meters per second, this change in velocity, negative 5 meters per second—final velocity— from 1 meter per second—initial velocity— that occurs in zero time because the time difference is 2 minus 2 and so that means we are dividing by 0 and so negative 5 meters per second— final velocity—minus 1 meters per second—initial velocity— that's negative 6 but we are dividing by 0 seconds, that is, you know, 2 minus 2, you might say 2 seconds minus 2 seconds which is 0 and dividing by 0 is undefined or in this case, you might say, negative infinity as this denominator approaches 0. So that's weird and that reflects the fact that the velocity changed instantly in which case you would require an acceleration of infinite proportions. So we can draw a little spike at 2 and that spike is gonna be in the negative direction. And up until that point, the acceleration was 0 so we are gonna be along the x-axis here up until 2 seconds and then it's an instantaneous spike downwards and then returning back to 0 again because the velocity is not changing at all during this time interval since the slope is constant to the position-time graph that means the velocity is constant and when velocity is constant, acceleration is zero and so we are in this little portion here where anywhere, the velocity is horizontal, there is zero acceleration. Okay. And so most of the time, it's horizontal and so most of the time, it's zero acceleration with the exception of these particular instance where you have a change in velocity just here and just here and here. Okay. So we are gonna go back to zero acceleration again until 3 seconds at which point there's a positive infinite acceleration back down to zero again and then carrying along until until we get to 5 seconds and then there's a positive infinite acceleration again. So there we go.