Question
A steel ball is dropped onto a hard floor from a height of 1.50 m and rebounds to a height of 1.45 m. (a) Calculate its velocity just before it strikes the floor. (b) Calculate its velocity just after it leaves the floor on its way back up. (c) Calculate its acceleration during contact with the floor if that contact lasts 0.0800 ms () . (d) How much did the ball compress during its collision with the floor, assuming the floor is absolutely rigid?
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 56 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
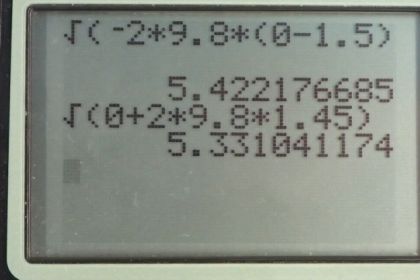
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A ball is dropped from an initial height of 1.5 meters and part (a) of this question asks what will its speed be when it reaches the ground? In part (b), it's going to be bouncing back up to some height which we call y 2 which is 1.45 meters and the part (b) is asking what velocity did it rebound with from the ground? And then part (c) asks us for the acceleration and part (d) is kind of interesting, it's asking us how much is this ball gonna be compressed? So let's begin with the velocity when it reaches the ground after falling 1.50 meters. So equation 77 tells us that the final velocity squared is the initial velocity squared minus 2 times acceleration due to gravity times the final height minus the initial height. Well, the initial velocity is zero because it's dropped meaning it's not given any downward initial velocity so v naught is zero so this term disappears. And then we take the square root of both sides to solve for v 1 and that is the plus or minus square root and we have to decide from the physics of the situation which sign it should be. Now since the steel ball is falling downwards, we usually take down to be the negative direction and up to be the positive direction so that means v 1 is going to be negative velocity because this thing is moving downwards here. And so we take the negative of the square root of negative 2 times 9.80 meters per second squared multiplied by the final height which is 0 meters at this ground level here minus the initial height of 1.50 meters this works out to negative 5.42 meters per second is the velocity of the steel ball when it hits the ground initially. Now this rebound from the ground is not perfectly efficient and so when it rebounds back upwards, the velocity that it will have will be a little bit less than the velocity it had when it hit the ground initially. So when it hits the ground, it has some velocity which we'll call v 1— this we figured out in part (a)— but when it rebounds, we'll call it v and we'll still give it a subscript 1 because it's at this position we have labelled with 1's here but it's not the same as this velocity so we need to distinguish it with a prime symbol. So this is v 1 prime, that's the velocity of the steel ball on the way back up after hitting the ground. And this velocity up here we'll call v 2 this is the maximum height that it reaches after rebounding, which we are told is 1.45 meters, and when something gets to its maximum height, its velocity is always zero so v 2 is 0 meters per second. And this v 2 squared equals the initial velocity, v 1 prime squared, minus 2g times the final height, y 2, minus the initial height, y 1— that's equation 77 again. Now we wanna solve for v 1 prime so we'll add 2g times y 2 minus y 1 to both sides and then these terms make zero and then we switch the sides around and take the square root of both sides and well, we end up with v 1 prime is square root of v 2 squared plus 2g times y 2 minus y 1. And that is the square root of 0 meters per second squared plus 2 times 9.80 meters per second squared times the final height of 1.45 meters minus the starting height at the ground of 0 meters which is a velocity of 5.33 meters per second. Now notice this is also plus or minus as it always is when you take the square root of both sides and we chose positive for our sign because from the physics we know that this ball is moving upwards after hitting the ground. Okay. The acceleration while in contact with the ground is the part (c) question. So that is the change in velocity divided by time— that's the definition of acceleration— and so that will be the final velocity which is the velocity that it rebounds with going upwards, v 1 prime, minus the initial velocity that it has going downwards, v 1, so that's 5.3310 meters per second— that's what we figured out in part (b)— minus the initially negative velocity, v 1, negative 5.42218 meters per second all divided by the time in contact with the ground which is 0.0800 milliseconds and 'milli' is times 10 to the minus 3. So this is 1.34 times 10 to the 5 meters per second squared— that's the acceleration— and that's positive because the velocity is changing in the upward direction. Then in part (d), we want to know what is the compression of the ball. So we are going to follow a point at the very top of the ball say and it has an initial velocity when the ball is just barely beginning to contact the ground; it's gonna have an initial velocity of negative 5.42218 meters per second— this was labeled v 1 before but we are gonna change our subscripts for part (d) and we'll just call this the initial v naught— and so that's the speed that the ball is contacting the ground with. And it has some height y naught; we don't really know what this y naught is because we don't know what the diameter of the ball is but it doesn't matter because we just want to know how much this this diameter changes. So we also know that this point is accelerating upwards and it's nevertheless moving downwards despite the acceleration upwards because the acceleration just started and it will be applied for sometime until this point at the top of the ball finally reaches a velocity of 0 and so this is the amount of compression here, this difference between the y, which is where this point at the top of the ball reaches when it's finally at a velocity of 0 versus where it started when it had a velocity of negative 5.4 meters per second down and so this is the amount of compression. So we can use equation 54 to figure this out; we know that the final velocity of this point at the top of the ball, which is zero when it's finished compressing, equals the initial velocity that it had squared plus 2 times its acceleration multiplied by its change in position. This is equation 54 and I don't use equation 77 because equation 77 presumes free falling in the downward direction and that's a negative acceleration but in this case, the acceleration is in fact positive because it's accelerating upwards and we are ignoring the acceleration due to gravity because it's really small in comparison to this huge acceleration due to contact with the ground. So we are gonna solve for y minus y naught and we'll subtract v naught squared from both sides, this v is zero and then we are dividing both sides by 2a and switching the sides around, we get y minus y naught equals negative v naught squared over 2a. And then we want to know what y naught minus y is just to get a positive answer because we know it starts off with a large diameter y naught and then compresses to a smaller diameter y so multiply both sides by negative 1 and so y minus y naught equals v naught squared over 2a. So that's negative 5.42218 meters per second squared divided by 2 times the acceleration of 1.344 times 10 to the 5 meters per second squared giving a compression of 1.09 times 10 to the minus 4 meters; that's about 0.109 millimeters.