Question
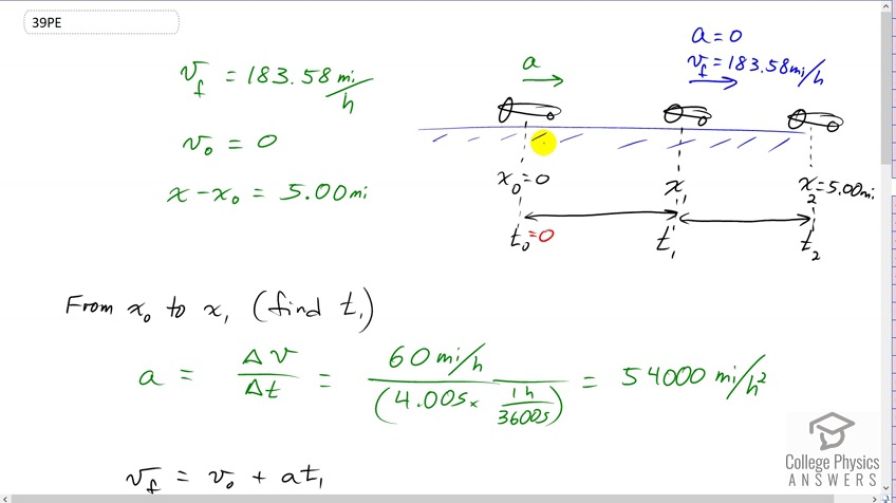
In 1967, New Zealander Burt Munro set the world record for an Indian motorcycle, on the Bonneville Salt Flats in Utah, with a maximum speed of 183.58 mi/h. The one-way course was 5.00 mi long. Acceleration rates are often described by the time it takes to reach 60.0 mi/h from rest. If this time was 4.00 s, and Burt accelerated at this rate until he reached his maximum speed, how long did it take Burt to complete the course?
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
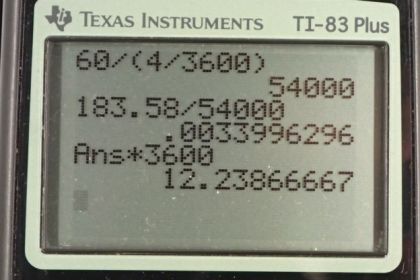
This is College Physics Answers with Shaun Dychko. The drag racer starts at position x naught equals 0 and time t naught equals 0 and it accelerates until it reaches this position here. And, we don't know what that position is, but we'll label it x1 and at a time t1. And the things we know about this position are that its acceleration is 0 at that point, because it has reached its final maximum velocity of 183.58 mph and then it maintains that velocity for this portion of the trip. So, we have two portions of the trip to consider. We have the portion here at the beginning when acceleration is something and non-zero. And then... And then we have the second portion here where the acceleration is 0. That because our formulas only work for constant acceleration, we need to consider this question in two stages because this question has non-constant acceleration which is what makes it a bit tricky. So, we reduce it down to two questions. One question involving this interval here during which acceleration is constant and then we consider the second interval here, during which acceleration also is constant. So, we've turned this problem that has non-constant acceleration overall into two different problems each of which does have constant acceleration within the intervals. Okay. So, we're going to consider this interval from x naught to x1 first and we will determine what this time t1 is. Ultimately, this question is: What is t2? That's the goal here. So, first, we'll figure out what t1 is and we know that the acceleration of the dragster is such that it reaches 60 mph within 4 seconds. And acceleration is change in velocity or change in time. And normally, I would change our units into MKS units - meters, kilograms and seconds, but there are so many miles an hours sprinkled throughout this problem that I'm just going to keep it in miles an hours. So, we have 60 miles per hour in the top divided by 4 seconds. Now, I'm just kind of contradicting myself a little bit. We have to keep units within the formula the same. And so, if we're going to have miles per hour in the top, we need to change the denominator units into hours also. So, we're multiplying this 4 seconds by a conversion factor of 1 hour for every 3600 seconds, leaving us with hours in the denominator. So now, these units match. So, that's good. And this works out to 54,000 miles per hour squared. It's the acceleration of the dragster. So, every hour, its speed would increase by 54,000 miles per hour. Then, we use this kinematic formula: final velocity equals initial velocity plus acceleration times time. And I've written this t1 here because that's this time. And we're going to solve for t1 by subtracting v naught from both sides and then switching the sides around. So, we have acceleration times t1 equals v f minus v naught. And then, divide both sides by a. And we have t1 that is v f minus v naught over a. So, it's 183.58 mph which is the maximum speed it reaches at this point minus the initial speed of 0, divided by 54000 mph squared acceleration that we just calculated here. And that works out to 3.3996 times 10 to the minus 3 hours. And I know it's hours because we have hours in our units here in the question. So, it's kind of a weird unit hours. So, let's change that into seconds and multiply it by 3600 seconds per hour, giving us 12.239 seconds. Alright. So, lots of work, but still not done. We have to consider this second portion now from here to here. We need to figure out what t2 is eventually. So, from x1 to x2, we have an acceleration of 0 because it has reached its maximum speed and it won't get any faster than that. And, we're going to find out that... well, here's a formula, you know, involving t2 which we want to find. But, it also has another unknown in it which is x1. Although we did find t1, which is good. We did not find x1 yet. And so, we'll need to do that in order to use this formula. But otherwise, we know everything else. We know that x2 is 5.00 miles. We know that... We know what t1 is because we calculated it. And we know the final speed. The question gives us that. Alright. So, let's find x1 then. So, x1 is the initial position of 0 plus v naught times t1 minus t naught, but that doesn't really matter because it starts at rest in that very first portion of time here. And... So, we're... this little section in green here is going back to the interval between x naught and x1 by the way. And, that's why we have 0s and 1s for our subscripts here. And... And plus one-half a times the time interval squared, time interval being t1 minus t naught. Now, v naught is 0. So, this whole term disappears. And then, t naught is zero as well because our initial time is 0. And so, this equation reduces to one-half a times t1 squared. x naught also being 0. So, that's one-half times 54000 miles per hour squared times 3.3996 times 10 to the minus 3 hours whole squared, giving us .31205 miles. That is the position x1. Then, we can return our attention to this formula and do some algebra to solve for t2 because we know everything in this formula except for the t2 term. So, we'll subtract x1 from both sides. And then, switch the sides around. And we have the v f times t2 minus t1 equals x2 minus x1. And dividing both sides by v f, we have t2 minus t1 equals x2 minus x1 over v f. And then, we'll add t1 to both sides, giving us this formula here. And now, we plug and check. We put in 5.00 miles for our final position x2 minus the position x1 that we calculated. .31205 miles divided by the final speed of 183.58 miles per hour plus the t1 which is 3.3996 times 10 to the minus 3 hours, giving us this many hours which we convert into seconds by multiplying by 3600 seconds per hour for a total time t2 of 104 seconds.