Video Transcript
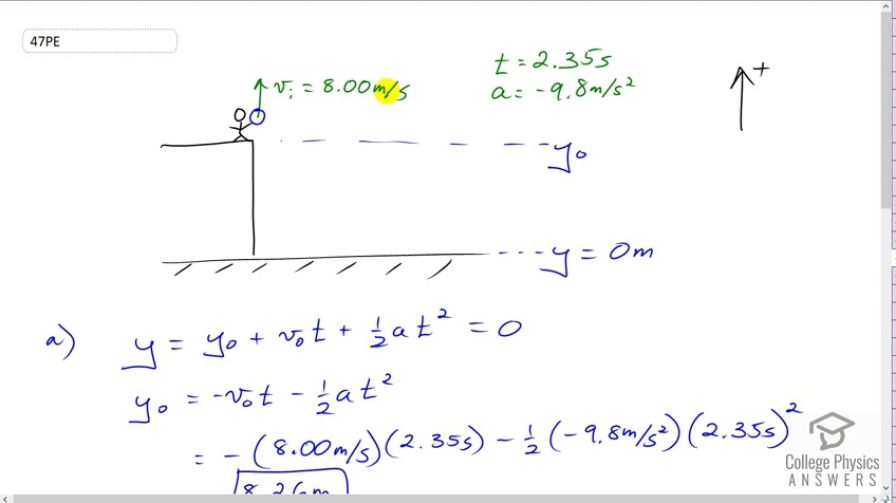
This is College Physics Answers with Shaun Dychko. This person is standing on a cliff and they throw a ball straight upwards with a velocity of positive 8.00 meters per second. We're going to take our coordinate system having positive being in the upwards direction. The ball eventually goes in this arc and hits the ground below the cliff 2.35 seconds later. The acceleration of the ball is that due to gravity which is directed downwards at 9.8 meters per second squared. The word downwards translates to this negative sign there, for the acceleration. Our job is to figure out what is the height of this cliff. Now, we're going to assume that the bottom of the cliff is our height zero and that'll be convenient because in this work we do here, that will make y naught become a positive number. We could have taken y naught equal to zero and then in this work we would have had, we would have been solving for y and it would have been a negative number. A height is usually expressed as a positive and so, we've chosen our coordinate system to have zero at the bottom such that when we workout our answer, we get a positive number. So we know that the the final position of this ball is going to equal its initial position plus the initial velocity, times the amount of time it takes to finish its trip, plus one half its acceleration, multiplied by time squared. Now, this equals zero because we've defined the final position to be zero, in which case we can subtract v naught t and and subtract one half at squared from both sides. We end up with negative v naught t minus one half at squared on the right side and we have y naught on the left side. So we subtract negative, we subtract v naught t from this side and one half at squared as well. So, now we plug in numbers and we have a minus from our formula there. Minus positive 8 meters per second for initial velocity, multiplied by 2.35 seconds, minus one half times negative 9.8 meters per second squared acceleration due to gravity, times 2.35 seconds squared. This gives positive 8.26 meters. So the height of the cliff is 8.26 meters. In part B, it's a different type of question where we're going to presume that we know what the height is, that we calculated in part A, and we'll say that the ball is now thrown downwards initially instead of being thrown upwards. The difference is that the initial velocity will now be negative because it was directed down. We're asked to find out what time would it take for the ball to hit the ground at the bottom of the cliff. We have the final position yequals zero again. So using this same formula up here, plugging in a zero for the final position y, we have equals y naught plus v naught t plus one half at squared. This is a quadratic equation and we can solve it using the quadratic formula. This is the generic form of a quadratic equation, some factor times the variable squared, plus some other factor b times the variables to the power of one plus some constant term c. The solution for this to find out what x is, is negative b plus or minus the square root of b squared, minus 4ac, all of that divided by 2a. So, what we need to do here is plug in some numbers and figure out which number is going to be the letter a, which number is going to be the letter b and which number will be the letter c and then plug it into this quadratic formula. So we have, I'm rearranging the terms a little bit, and so I put the squared term first because that looks more similar to what I'm used to here with this quadratic equation. So we have one half times the acceleration, negative 9.8 meters per second squared, times t squared, plus negative 8 meters per second, times t plus the height of the cliff, 8.2603 meters and then multiplying by half there. That's the only change in this line here is that the one half negative 9.8 became negative 4.9. Now, it is of the form of the quadratic equation. So now we can see which factors here correspond to which letters over here. The a is negative 4.9, the b is negative 8, and the c is 8.2603. And so, we make the substitutions here. So we have a negative in the formula, times negative 8.0 meters per second, plus or minus the square root of negative 8.0 meters per second squared, minus 4 times a which is negative 4.9. The a here of course, is not acceleration a, it's just the factor times x squared. It worked to being half of the acceleration due to gravity here. That gets multiplied by 8.2603 meters which is the constant term c, and all divided by 2 times negative 4.9 meters per second squared. And so this gives two answers, one with taking a plus here, and another with taking a minus. When you take a plus, you get a negative 2.35 seconds, and taking the minus, you get positive 0.71735 seconds. It doesn't make physical sense to have a negative time. So we're going to take this to be our answer. It makes sense because we expect this number to be smaller than the time we had in part A. In part A, the ball was initially thrown upwards and so it should take a longer time to hit the ground and it took 2.35 seconds. And so for part B with the ball being thrown downwards initially, we expect the time to be less. And so it's always good to do a reality check on your answers to see if they make sense. And here being less than 2.35 seconds, I can believe it. So, here we are. Our answer is, time is 0.717 seconds if the ball is initially thrown downwards from the cliff.