Question
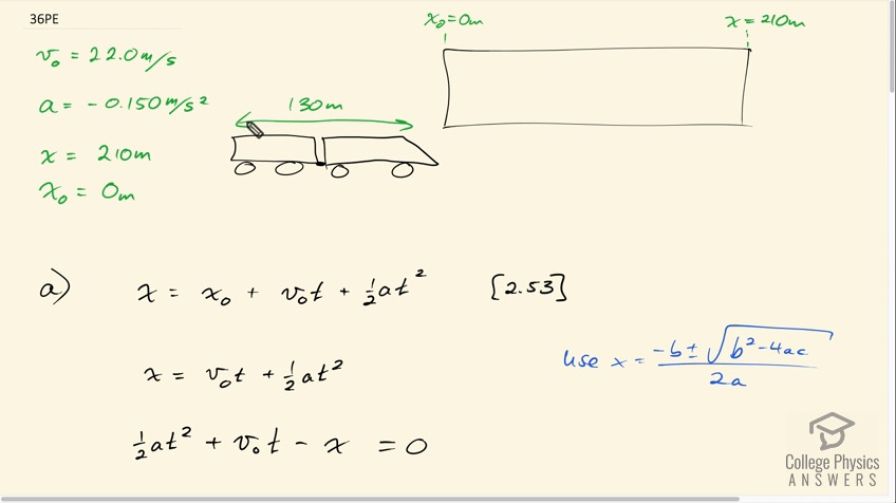
An express train passes through a station. It enters with an initial velocity of 22.0 m/s and decelerates at a rate of as it goes through. The station is 210 m long. (a) How long is the nose of the train in the station? (b) How fast is it going when the nose leaves the station? (c) If the train is 130 m long, when does the end of the train leave the station? (d) What is the velocity of the end of the train as it leaves?
Final Answer
Solution video
OpenStax College Physics, Chapter 2, Problem 36 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
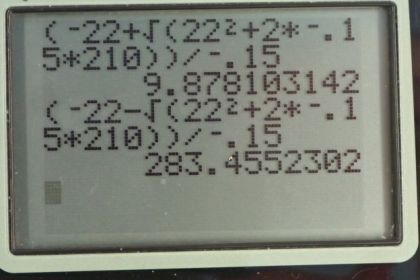
This is College Physics Answers with Shaun Dychko. A train is approaching a train station and the train station is 210 meters long; the train's initially traveling at 22 meters per second and it has a deceleration of 0.150 meters per second squared and deceleration means that the acceleration is in the opposite direction to the initial velocity. So with the initial velocity being taken to be positive, so that means to the right is positive in this picture, that means acceleration must be to the left and so that's why there's a negative sign there. And the initial position we'll take to be zero at the start of the station and the final position will be 210 meters. So that's writing down all the things that we know and also drawing a picture. So part (a) asks us to figure out how long is the nose of the train in the station? So we have equation 53 says that the final position equals the initial position plus initial velocity times time plus one-half times acceleration times time squared and this term here will disappear because we have x naught equal to zero but the other terms remain and this is going to be a quadratic equation and we'll need to use a quadratic formula to solve it. So we subtract x from both sides here and then collect everything on the left side equals 0 on the right side. So this is of the form of a quadratic equation where the unknown is squared and then the unknown has a power of 1 and then the unknown has a power of 0 if you like to say that, you know, you could imagine that there's t to the power of 0 here which is just the number 1. Okay. And this term here doesn't necessarily have to be there but it is in this case and if it was not there, we could just take the square root of both sides after solving for t squared but since this term is here, we need to use this handy quadratic formula. So we say that the unknown, which is t in this case, equals the negative of the coefficient of the linear term which is the term where the unknown has the exponent 1 and so that's going to be negative v naught written here plus or minus the square root of v naught squared and then minus 4 times the coefficient of the squared term which is one-half a times the constant term which is just this number left over here which is the number negative x. And so I substituted negative x in here but I didn't write it that way, I just made this into a plus sign because this minus from the quadratic formula and the negative in front of the x combine to make this positive here. Okay. And then we divide by 2 times the coefficient of the squared term which is one-half a. So we simplify it a little bit by multiplying the 4 by a half to make 2 and then the 2 by a half down there to make 1 and we have this formula for solving for t. So we substitute in the numbers now; we have negative 22 meters per second plus or minus square root of 22 meters per second squared plus 2 times negative 0.150 meters per second squared—acceleration— multiplied by the final position of 210 meters all divided by negative 0.150 meters per second squared. And this will give you two answers; 9.8781 seconds or 283.455 seconds and you get the two different answers depending whether you took the plus or the minus there and so the question becomes which answer is correct? Well they are both mathematically correct that's why you are getting two answers in your calculator but one is physically correct because the first time that this nose passes this position here will be 9.88 seconds and the interpretation of the second number is that well, if once the nose passes, the train if it continues to decelerate and decelerate and decelerate, it will turn eventually turn around and start going backwards and then the nose will pass this position once again going in the reverse direction after 283 seconds. So there's usually a meaning, an interpretation for these multiple answers to this quadratic formula and that's the interpretation here. So we want to know when is the first time that the nose will pass the station going in the direction of the initial velocity to the right and the answer to that is 9.88 seconds and so this is going to be extraneous. So part (b) asks us how fast is it going when the nose is here? And so it's going to be some speed slower than 22 meters per second so when we get our answer, we are going to compare with 22— we are always going to do a reality check when there's something to compare it to— and we expect an answer less than 22. We are going to use equation 54 which says that the final velocity squared equals the initial velocity squared plus 2 times acceleration multiplied by the change in position. So we take the square root of both sides and solve for final velocity. So we have square root of 22 meters per second squared plus 2 times negative 0.150 meters per second squared—acceleration— multiplied by 210 meters—final position— minus 0 meters—initial position— giving us 20.5 meters per second is the final velocity and that is indeed less than 22 meters per second as we expected and that adds to its believability. And then part (c) asks us if the train is 130 meters long, when does the end of the train leave the station? So at what time does this point here reach the end of the station? So we need to redefine our x naught and our x; our initial position, we'll take to be the rear of the train and that's, you know, just for convenience because you know this is point that's moving that we are interested in and let's take its initial position to be zero and then its final position will be the 210 meters— length of the station—plus the 130 meters—length of the train and so it's final position is 340 meters compared with our initial position here which is the end of the train at the beginning of the time period. Okay. So x naught is 0 and x is now 340 meters. So we can use the same formula that we had over here we solved for t before and found negative v naught plus or minus square root of v naught squared plus 2ax over a and we'll just rewrite that here but with different numbers now; this 210 meters has now become 340 meters— everything else is the same as for part (a), now there's no longer 210 there. And this works out to 16.368 seconds and 276.97 seconds and this one is when the end of the train has passed the end of the station and then returned in the reverse direction and we'll reject that and we'll take this answer, 16.4 seconds. Part (d) asks what is the velocity of the end of the train as it leaves? And so we use the same formula as we did for part (c) but now instead of 210 meters, our final position is 340 meters and this works out to 19.5 meters per second.