Video Transcript
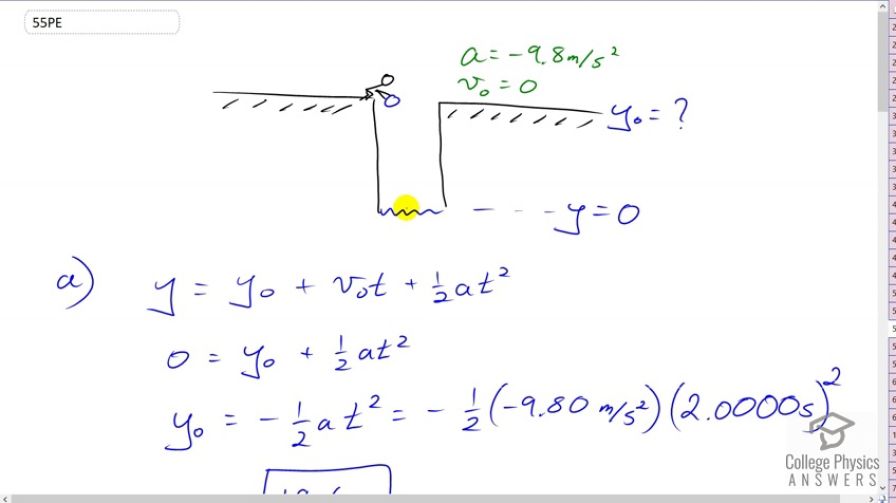
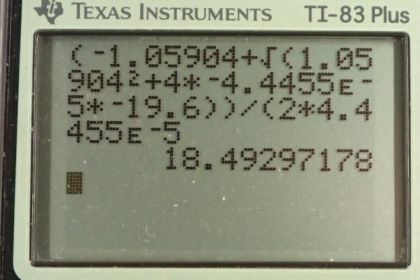
This is College Physics Answers with Shaun Dychko. A rock is dropped into a deep well and the sound of it hitting the bottom is heard 2 seconds later and our job is to calculate what the height of the well must be. In Part A, we assume that we hear the sound at the very moment when the rock hits the water. So we assume that it takes no time for the sound to get back to our ears from the water. So that's a bit of a simplification. It makes the work a lot easier. But it works out to making our calculation for the well depth a bit bigger than it should be. So let's say that the final position of the rock will equal the initial position plus its initial velocity times time, plus one half times acceleration times time squared. The final position is zero and the initial position is we don't know. That's what we want to find 'cause that will also be the height of the well. The initial velocity is zero because the rock is just dropped, it is not thrown down. Then we have this plus one half at squared. The term is still there. So we'll subtract one half at squared from both sides and switch the sides around leaving us with y naught equals negative one half at squared. So it's negative one half times the acceleration due to gravity of negative 9.8 meters per second squared, times the time of 2.0000 seconds squared, giving us 19.6 meters is the depth of the well assuming we hear the sound instantly when the rock hits the bottom. Now, in part B, we make it a little bit more sophisticated our analysis because we're going to say that it does take time for the sound to go from the water back to our ears. So this 2.0000 seconds time that we measure is going to be the total of two time intervals. One time interval t one we'll call it delta t one, delta meaning interval or difference. This delta t one is going to be the time it takes for the rock to hit the water and we don't know what that time is. Then delta t two is going to be the time it takes for sound to go from the water back to our ears. What we know is the total of delta t one plus delta t two and that is 2.0000 seconds. Anyway, so we write down the stuff that we know. We know the speed of sound is 332 meters per second. We know acceleration. We know initial velocity is zero and we have our final position is zero at the bottom of the well and our initial position is y naught which we want to find. We also don't know what delta t one is, nor delta t two. Okay. So we write down some equations expressing relationships between different quantities and then we combine equations together to solve for the unknowns. So we don't know t one, we don't know t two, and we don't know y naught. So because there are three unknowns we are going to need three equations. That always works that way, that you need as many equations as there are unknowns to solve the system of equations. It's called a system of equations when you have several different equations relating to the same problem. Okay. So one equation we can use is that this y naught equals the speed of sound multiplied by the time it takes to get from the water to the person's ear. There is no acceleration involved because this is sound we're talking about. It is not affected by gravity. So we have y naught equals vs times delta t two. Then we know that the sum of the two time intervals is 2 seconds and now we'll make an expression for this time interval when the rock is dropped and it's accelerating down to the bottom of the well. We'll say that the final position y equals initial position y naught plus v naught times delta t one, plus one half times acceleration times delta t one squared. So this is delta t one here which we don't know, the interval of time from when the rock has dropped until it hits the water. Now we'll simplify this a bit by getting rid of the terms that are just zero. v naught is zero so this term disappears and the final position is zero so we have zero equals y naught plus one half a delta t one squared. Now we'll do some substitution to get rid of one of our variables here. This is an equation with two unknowns and so we can't solve it. We don't know what y naught is and we also don't know delta t one. So there's nothing we can do unless we have other equations to help us. So we want to make a substitution for delta t one and if we can make an expression that is in terms of y naught, and that being the only unknown in our substitution here, then we will be able to solve this equation because it will contain only one unknown, being y naught. So let's work on that. This equation is going to be helpful. It's going to say delta t one is two minus delta t two but that's not quite good enough because we also don't know delta t two. But we can use equation one to get an expression for delta t two in terms of y naught which is good. So it's y naught divided by vs where we divided both sides by vs here. Then looking at equation two we substitute for delta t two and replace it with y naught over vs. So we have delta t one plus y naught over vs equals two. Now we have, after you subtract y naught over vs from both sides, we have delta t one equals two minus y naught over vs. This is good stuff because if we plug it into equation three, we will have an equation containing only one unknown. So that's what we do in this line here where I've re-written equation three, called it three b and I've made a substitution for delta t one as two minus y naught over vs instead. The only thing we don't know in this equation is y naught and so we can solve it. We know what the speed of sound is and we know what the acceleration due to gravity is. Okay. I'm going to square this binomial and here's the pattern for squaring a binomial by the way. If you have one term minus another term all squared, the answer to that is going to be the first term squared, and minus two times the first term, times the second term, and then plus the second term squared. So we have the first term being two, so two squared is four, minus two times the first term, so two times two makes four, times the second term y naught over vs, and then plus the second term squared, y naught squared over vssquared. Then we multiply through by the one half a into each term in the brackets. We have one half times four makes two a and then minus two a y naught over vs and then plus a y naught squared over two vs squared. We're going to collect the linear terms together because we want to make this into the form of a quadratic equation because we have a quadratic formula that we can use to solve it. So we have the squared terms first. We have a y naught squared over two vs squared. I just moved it there, nothing special about that. The next part involves a little bit of work where I collected these two terms together by factoring out the common factor y naught. That gives us bracket one minus two a over vs then we have plus two a -- this term is just moved there -- equals zero. Then substituting in numbers, we have negative 9.8 y naught squared over two times the speed of sound, 332 squared -- normally I'd put units into everything but there is so much numbers, so many numbers here that that's too much work. So I'm just going to write numbers in this case. Most of the time I'll still do units. Then bracket one minus two times negative 9.8 over 332 y naught, plus two times negative 9.8, all equals zero. Then you do calculations there and it works out to these numbers which we then substitute into the quadratic formula. So we have the coefficient of the linear term negative, plus or minus the square root of the coefficient of linear terms squared, minus four times the coefficient of the quadratic term, multiplied by the constant term, and divided by two times that coefficient of y naught squared, negative by the way. This all works out to 18.5 meters and it turns out that you need to use the plus here. You can't really know that until you try one and then the other. If you use a minus, you get a really big negative number which doesn't have a physical interpretation here and so we take the positive answer. So there's the height or there's the depth of the well, 18.5 meters.