Question
(a) What is the mass of a large ship that has a momentum of , when the ship is moving at a speed
of 48.0 km/h? (b) Compare the ship’s momentum to the momentum of a 1100-kg artillery shell fired at a speed of 1200 m/s .
Final Answer
- The momentum of the ship is greater than that of the artillery shell by a factor of 1210.
Solution video
OpenStax College Physics, Chapter 8, Problem 2 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
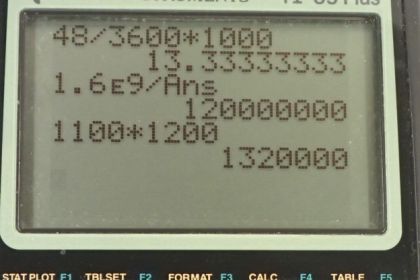
This is College Physics Answers with Shaun Dychko. A ship has momentum of 1.60 times 10 to the 9 kilogram meters per second and we are told its speed is 48.0 kilometers an hour and we need to figure out what its mass is. So we'll convert this speed into 'mks' units, which we usually need for most of our formulas— meters, kilograms and seconds. We'll multiply by 1 hour for every 3600 seconds that gets rid of the 'hours' units leaving us with seconds on the bottom and then we'll multiply by 1000 meters per kilometer and now we have meters on top and this is 13.333 meters per second. So our formula for momentum is that it's mass multiplied by velocity and so we'll divide both sides by v to solve for m and then switch the sides around as well so m is momentum divided by velocity. That is 1.60 times 10 to the 9 kilogram meters per second divided by 13.333 meters per second and that is 1.20 times 10 to the 8 kilograms. In part (b), we are asked about an artillery shell so I have a subscript a to label this as belonging to the artillery shell and so its momentum is the mass of the artillery shell times the speed of the artillery shell... velocity technically but that's not an important distinction in this question between speed and velocity. So we have 1100 kilograms—mass— multiplied by 1200 meters per second and of course the speed is enormously greater than that of the ship but the mass is so much less that they end up with a momentum much less than that of the ship. So the momentum of the artillery shell is 1.32 times 10 to the 6 kilogram meters per second. And so we divide the momentum of the ship divided by the momentum of the artillery shell and we get 1210. So the momentum of the ship then is greater than that of the artillery shell by this factor of 1210.