Question
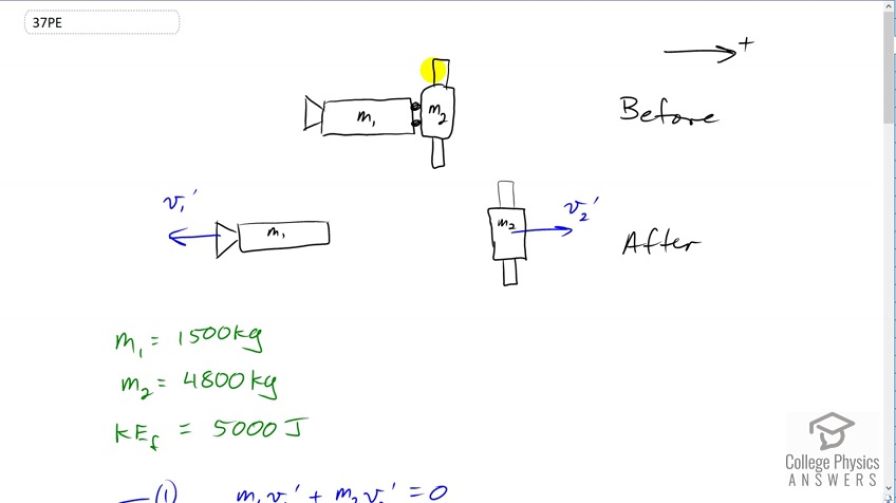
Space probes may be separated from their launchers by exploding bolts. (They bolt away from one another.) Suppose a 4800-kg satellite uses this method to separate from the 1500-kg remains of its launcher, and that 5000 J of kinetic energy is supplied to the two parts. What are their subsequent velocities using the frame of reference in which they were at rest before separation?
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 37 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
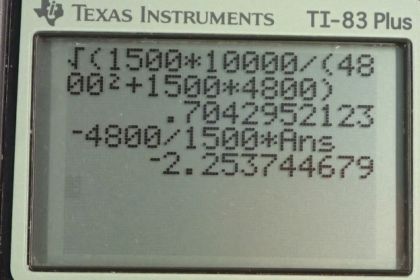
This is College Physics Answers with Shaun Dychko. This satellite here labeled m two and its launcher labeled m one, are connected with exploding bolts. We're going to consider this problem in the reference frame of the satellite launcher which means that initially there is zero velocity. Then sometime later the bolts will explode and that's going to send the satellite to the right and the launcher to the left. The velocities will be such that the total momentum of each of these pieces is going to equal zero because it had zero momentum to begin with. That is what we say in this first line right here. So the launcher mass is 1,500 kilograms, the satellite mass is 4,800 kilograms and we're told that the total kinetic energy of these two pieces after the explosion of the bolt is 5,000 joules. So, we're going to write down our conservation of momentum formula first. The total momentum of each of the pieces after the explosion equals the total momentum initially which is zero and we'll write down that the total kinetic energy is 5,000 after the explosion. We say that by writing one half m one v one prime squared, plus one half m two v two prime squared is 5000. So we have a system of equations and two unknowns. So it's a good thing we have two equations because that's the number of equations you need to solve for two unknown variables. So we're going to do some algebra to combine these equations to solve for them. Let's rearrange equation one and we're going to solve it for v one prime squared, and I did that because in equation two we have a v one prime squared. So we're going to create two equations for v one prime squared and once we do that we can equate those two things together and it will have only one variable, v two prime squared. We'll see that in a second. So equation one is, well we take this to the right hand side by subtracting it from both sides and by the way, this should be a minus there. Actually, not necessarily. I did two things at once here actually. When you move it to the right hand side, sure it gets a minus but then I squared both sides and so the minus disappears because negative m two v two prime times negative m two v two prime is positive m two squared v two prime squared. So this is correct. Then we divide both sides by m one squared there to solve for v one prime squared. Okay. That gives us this line and we cannot go any further than that. But we can turn our attention instead to equation two, the kinetic energy formula and rearrange that to solve for v one prime squared also. So I multiplied everything by two on both sides and the one halves canceled from the two terms on the left. Then the 5,000 joules becomes 10,000 joules and then I also moved this term to the right hand side by subtracting it from both sides. So that's negative m two v two prime squared is on the right side now. Then divide both sides by m one. We have v one prime squared is 10,000 joules minus m two v two prime squared divide by m one. So we have two expressions for v one prime squared and so that means these two things are equal to each other. We can say that equation one b is equal to equation to equation two b. So we can equate the right sides. We have m two squared over m one squared times v two prime squared from equation one b equals 10,000 joules minus m two v two prime squared over m one because each of these things is equal to v one prime squared. Now we're going to solve for v two prime. First of all, we'll -- what do we do first here? I multiplied everything by m one first, that's what I did, and then that makes the denominator here m one to the power one. I canceled the m one there and then this term, you can add it to both sides, plus m two v two prime squared and then add it to this side as well. Then it disappears on the right side and appears on the left. That equals 10,000. Then we factor out the v two prime square and then also multiply this term by m one over m one which we're allowed to do since m one over m one is the number one. You can multiply anything you like by one without changing its value, but we did it in order to change the way this looks so that we have a common denominator. I think that just looks nicer. So we have m two squared plus m one m two all over m one, multiplied by v two prime squared. Then multiply both sides by the reciprocal of that factor so multiply by m one over m two squared plus m one m two and do the same to the right side so that the equation stays balanced. Then we have this line here, v two prime squared is 10,000 times m one all over m two squared plus m one m two. Then take the square root of both sides. We get v two prime now, is equal to the square root of m one times 10,000 joules over m two squared plus m one m two. This is 1,500 kilograms times 10,000 joules divided by 4,800 kilograms squared, plus 1,500 kilograms times 4,800 kilograms. This gives 0.704 meters per second. So there we have solved for the velocity of the satellite. The velocity of the launcher, well, we get to that next. We have this equation here. From this conservation of momentum, actually, let's just look at this. From this conservation of momentum we can say that v one prime is negative m two v two prime over m one where I took this term to the right hand side and then divided both sides bym one. So that's what we're going to use to find v one prime because we now know v two prime. So that's what we do here. So v one prime is negative m two over m one times v two prime. So that's negative 4,800 kilograms divided by 1,500 kilograms times 0.704295 meters per second, including lots of digits there to avoid intermediate rounding error. We end up with negative 2.25 meters per second. This is negative because the launcher is moving to the left and we took right to be the positive direction.