Question
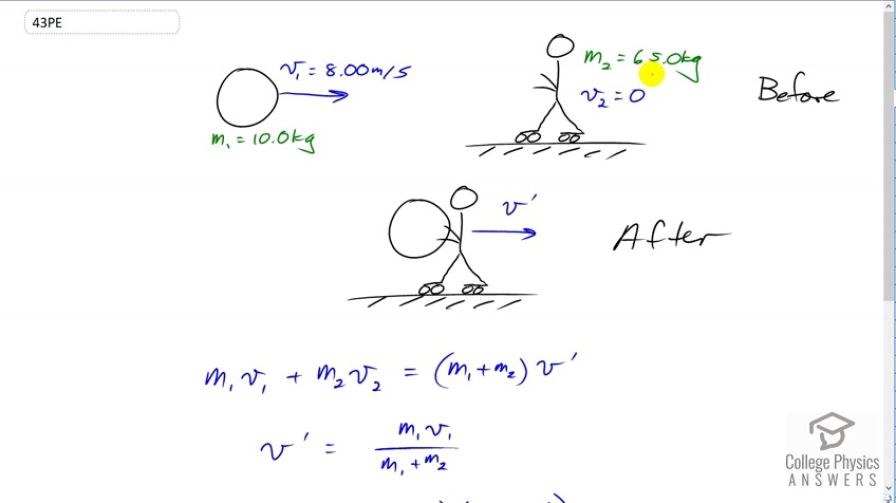
During a circus act, an elderly performer thrills the crowd by catching a cannon ball shot at him. The cannon ball has a mass of 10.0 kg and the horizontal component of its velocity is 8.00 m/s when the 65.0-kg performer catches it. If the performer is on nearly frictionless roller skates, what is his recoil velocity?
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 43 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This performer is on frictionless roller skates and initially at rest, so v two equals zero. The performer's mass m two is 65 kilograms and a cannonball is approaching them with a horizontal velocity of eight meters per second. The cannonball has a mass of ten kilograms. The performer will catch the ball and then the two things, the ball and performer combined, will move with some velocity v prime after the collision. So the total momentum before the collision which is the momentum of the cannonball plus the momentum of the performer, will equal the total momentum afterwards and that will be the combined mass of the two things that are stuck together, multiplied by their common velocity v prime. Now since the performer initially has no velocity, that means they have no momentum so this term is zero. We can divide both sides by m one plus m two and then switch the sides around so that we have the unknown on the left. So we solve for v prime is m one v one over m one plus m two. So this is ten kilograms times eight meters per second divided by ten plus 65 kilograms, giving us a velocity after the performer catches the ball, of 1.07 meters per second.
