Question
Squids have been reported to jump from the ocean and travel 30.0 m (measured horizontally) before re-entering the water. (a) Calculate the initial speed of the squid if it leaves the water at an angle of , assuming negligible lift from the air and negligible air resistance. (b) The squid propels itself by squirting water. What fraction of its mass would it have to eject in order to achieve the speed found in the previous part? The water is ejected at 12.0 m/s ; gravitational force and friction are neglected. (c) What is unreasonable about the results? (d) Which premise is unreasonable, or which premises are inconsistent?
Final Answer
- It is unreasonable to assume the squid can expel 83% of its mass.
- The 30.0 m range is unreasonable.
Solution video
OpenStax College Physics, Chapter 8, Problem 62 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
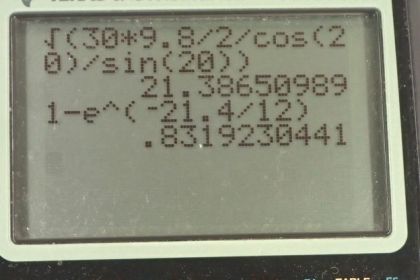
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A squid apparently launches itself from the water at an angle of 20 degrees and reenters the water 30 meters later so the range is horizontally 30 meters. Now we have a range formula in order to find this initial launch speed here but let's derive the formula just for fun. So the horizontal range is gonna be the horizontal component of this launch velocity multiplied by time and there's no acceleration horizontally because gravity is acting only vertically and so we have v times cos Θ is v x and we are multiplying that by time t. And we don't know v nor do we know t so that means we need to consider a second equation in order to solve for the two unknowns. So we have this vertical displacement then which is going to be zero because it's gonna return back to its same vertical position when it hits the water again that's going to be the initial y-component of its velocity multiplied by time minus one-half times acceleration due to gravity times time squared and because this all equals zero, we can conveniently divide everything by t and then we have gt over 2— it's not squared anymore because we divided by t— and this whole term can be moved to the right-hand side which makes it positive and then switch the sides around and we are left with v y-component initial on the other side. Now we are solving for t here so let's multiply both sides by 2 over g and then also make a substitution for the y-component as v times sin Θ because it's this opposite leg in this triangle here that we are looking for and now we have an expression for time and this can be replaced in place of t in this range formula which we do here. So the range then is the launch speed v times cos Θ times 2 times launch speed v again times sin Θ divided by g. And so the v's multiply together to make v squared on one side and on the other side, we'll multiply both sides by g over cos Θsin Θ also times 2 there and we get this line here: v squared is Rg over 2cos Θsin Θ. Now in the work we did with the range formula, we replace this with the trigonometric identity sin 2Θ but we don't need to do that, we'll just leave it the way it is. And we'll take the square root of both sides so v is the square root of the range times acceleration due to gravity divided by 2 times cos of the launch angle times sin of the launch angle. So that's 30.0 meters times 9.80 meters per second squared divided by 2 times cos 20 times sin 20 and all that works out to 21.4 meters per second. And part (b) says what fraction of the squid's mass has to be ejected given a certain speed of the exhaust of 12.0 meters per second in order to reach this final speed that's been reported. So equation 80 from chapter 8 will help us out here: divide both sides by the exhaust velocity and we have natural logarithm of the original mass of the squid including the propellant divided by the mass of squid that's leftover after the propellant is finished being ejected equals the final velocity of the squid divided by the velocity of the propellant. Make both sides exponent's for the exponential and doing that on the left gets rid of the natural logarithm and we are left with m naught over m and on the right side, we have e to the power of v over v e. Then raise both sides to the exponent negative 1 to get this fraction as m over m naught and that equals e to the negative v over v e. Now the fraction ejected is gonna be the original mass minus the mass leftover divided by the original mass and you can divide both terms by the m naught and that gives us 1 minus m over m naught and this is what we just found an expression for here so we'll replace it with e to the negative v over v e. So we have 1 minus e to the negative 21.4 meters per second divided by 12.0 meters per second which is 0.832. Now it's unreasonable to think that a squid can eject 83% of its mass and so the 30.0 meter range that was reported must be unreasonable.