Question
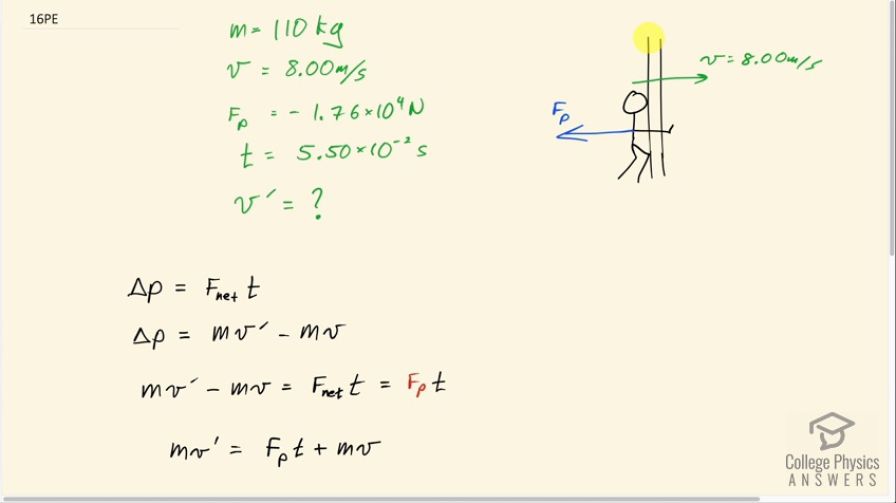
Calculate the final speed of a 110-kg rugby player who is initially running at 8.00 m/s but collides head-on with a padded goalpost and experiences a backward force of for .
Final Answer
Note: While the video solution correctly finds the final velocity, the question is in fact asking for the final speed. We just take the magnitude (make it positive in other words) of the final velocity to get the final speed. Thank you Bethany Bonjovi for pointing this out in the comments.
Solution video
OpenStax College Physics, Chapter 8, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A rugby player is initially going 8.00 meters per second to the right in this picture and they collide with a padded goal post which exerts a force backwards on the rugby player, we'll call that F P for 'post'. And we are told that that force is 1.76 times 10 to the 4 newtons and the mass of the rugby player is 110 kilograms and this post force is applied for 5.50 times 10 to the minus 2 seconds. And I have labeled this initial velocity v and the final velocity that we want to find is v prime. Okay! So the change in momentum of the rugby player will be the net force on them multiplied by time—this is the impulse formula— and you could also write the change in momentum as the final momentum minus the initial momentum where we have mass times final velocity minus mass times initial velocity here. So since both of these equal the change in momentum, we can make them equal to each other which we do in this line here so mv prime minus mv equals F net times t. And then we substitute the force exerted by the post in place of the net force because this is the only horizontal force in this picture and so that is the net horizontal force; we can ignore gravity and normal force because they are vertical and independent. So we add mv to this side and to this side to isolate mv prime here on the left— mv prime equals F P t plus mv— and then divide both sides by the mass and we get a formula for the final velocity. So that's the force exerted by the post multiplied by time plus mass times initial velocity all divided by mass. So that's negative 1.76 times 10 to the 4 newtons times 5.50 times 10 to the minus 2 seconds plus 110 kilograms times 8.00 meters per second divided by 110 kilograms making a final velocity of negative 0.800 meters per second. The negative sign indicates that the rugby player is bouncing off this post and they will be going to the left in this picture after the collision.
Comments
Hi, can the final speed be negative?


