OpenStax College Physics, Chapter 8, Problem 54 (Problems & Exercises)

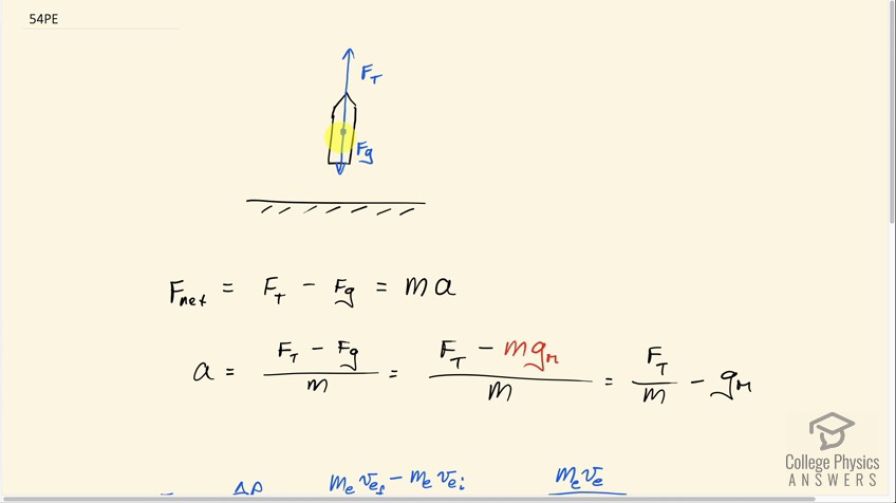
This is College Physics Answers with Shaun Dychko. A rocket is accelerating off the surface of the Moon and there's going to be a thrust force upwards and a force of gravity downwards and that means the net force then is thrust up minus gravity down and that's going to be equal to the mass of the rocket times its acceleration. We have to figure out what a is and we'll solve for it by dividing both sides by m and then switching the sides around. So we have acceleration is thrust force minus gravity divided by rocket mass. And we can substitute for gravity by writing the mass of the rocket multiplied by the acceleration due to gravity on the Moon which we are given is 1.6 meters per second squared and then we'll divide m into each of these terms and write this as thrust force divided by rocket mass minus acceleration due to gravity on the Moon. So then we have to think about how to calculate this thrust force. Now this thrust force is the force exerted on the rocket due to the exhaust particles so there's exhaust coming out the bottom end of this rocket here and in order for this exhaust to shoot out the bottom, the rocket needs to exert a force on the exhaust and then the exhaust in turn has a Newton's third-law counterpart or reaction force on the rocket of the same magnitude but upwards. So the rocket's forcing the exhaust down and then the exhaust is in turn forcing the rocket up. Okay! So this means the thrust force is gonna be equal to the rate of change in momentum of the exhaust. Now this is Newton's second law written in actually the original form that Newton wrote it in which is to say that net force is the rate of change of momentum and you could rewrite this as mass times acceleration, if you wanted; it's the same thing. But it's useful to write it this way because we can talk about the momentum of the exhaust particles and so the change in momentum of the exhaust is going to be the mass of the exhaust expelled multiplied by its final velocity minus the mass of the exhaust expelled multiplied by its initial velocity. Its initial velocity is zero because it's at rest inside the rocket in the gas tank and so this simplifies to m ev e over Δt. Now we know all these things: we know the rate at which mass is expelled is 8 kilograms per second so mass is 8.00 kilograms and Δt is 1.00 second and we also know the speed that it comes out at— 2.20 times 10 to the 3 meters per second. So we can plug all this stuff in for F T in our acceleration formula and I have rewritten that here. So we have acceleration then is mass of the exhaust expelled multiplied by the velocity of the exhaust divided by the mass of the rocket times Δt minus acceleration due to gravity on the Moon. So that's 8.00 kilograms times 2.20 times 10 to the 3 meters per second divided by 5000 kilograms— mass of the rocket— multiplied by 1.00 second minus 1.60 and that gives 1.9 meters per second squared is the acceleration of the rocket.