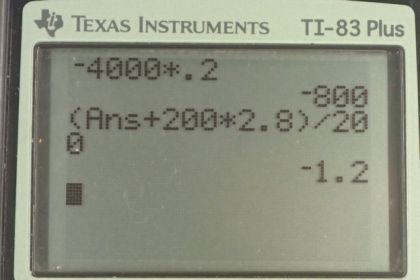
a)
b)
Solution video
OpenStax College Physics, Chapter 8, Problem 11 (Problems & Exercises)
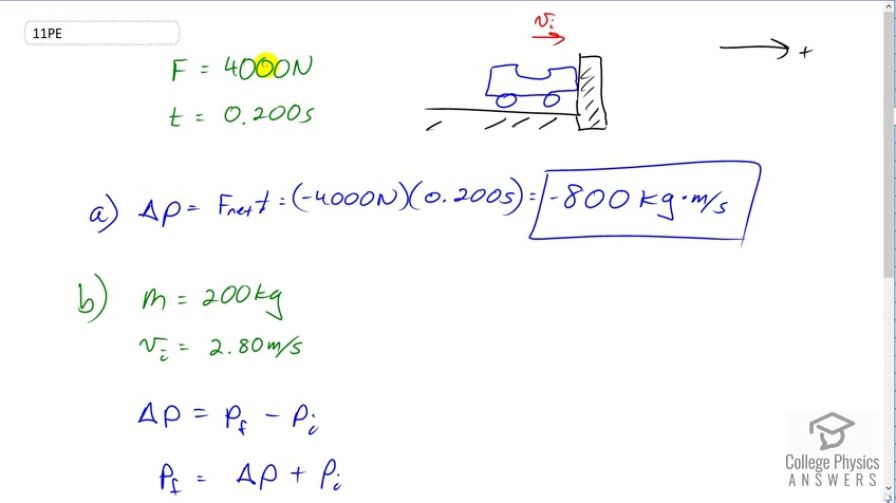
Calculator Screenshots
Comments
Hello Shaun,
Thank you for your helpful videos. I am studying from your website right now and this is my first comment.
Why did you assume that the force on the car by the side rail is in the negative direction? I assumed it is in the positive direction (because the question left it ambiguous) and got a completely different answer in part b.
Hello PlaywtPhysics,
I'm really glad you're finding the videos helpful! Thanks for the comment. I assume you got a different answer for part (b)? It's fine to choose the coordinate system however you like. Choose left to be positive is fine. Regardless of the choice of coordinate system, it's very important to be consistent. Choosing left as positive would mean the initial velocity to the right is negative. Could you check for that in your work?
All the best,
Shaun
You are right. I forgot to account for the direction of the initial velocity, which is negative according to the coordinate system I picked.
Is it typical for physics problems to give you the magnitude of things, and then it's up to you to take care of the signs that follow from your own diagrams?
Awesome, glad it's figured out. Yes, it's typical that the student is left to sort out the signs, whereas the question will usually use words to indicate direction, such as "left" or "right". For one, it's more readable with words, but additionally, a negative sign would be ambiguous unless the question explicitly establishes the coordinate system. Doing so for every question would be tedious. Now that you understand the issue, I think you're in good shape.
Best wishes with your studies,
Shaun