Question
Two piloted satellites approach one another at a relative speed of 0.250 m/s, intending to dock. The first has a mass of , and the second a mass of . If the two satellites collide elastically rather than dock, what is their final relative velocity?
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 29 (Problems & Exercises)
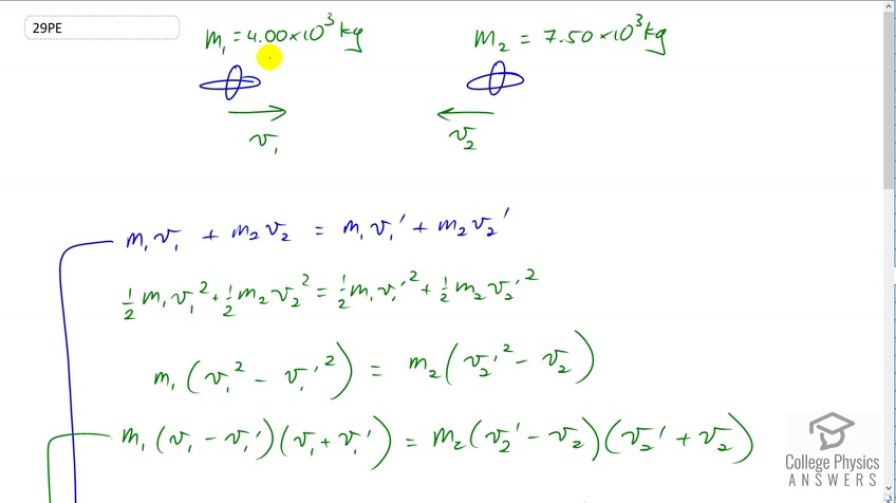
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College physics Answers with Shaun Dychko. These two satellites are going to have a perfectly elastic collision. This first one has a mass of four times ten to the three kilograms and the second one has a different mass, but the masses don't actually matter for our answer as to the relative velocity after collision. So we have that this velocity is to the right and this velocity is to the left say, and we know that momentum will be conserved in the collision. So that means mass one times v one plus mass two times v two before collision, that total momentum before the collision will equal the total momentum after collision, where I have v one prime and v two prime, each with a prime symbol to denote after collision. Since this is a perfectly elastic collision, it means the total kinetic energy will also be conserved. So this is the kinetic energy of the first satellite and here's the kinetic energy of the second satellite, both before collision and that total will equal the kinetic energy of the first satellite after collision plus the kinetic energy of the second satellite after collision. We're going to -- we're given what the relative velocity is between these two satellites. We're not told what the velocities are, but we're told that v oneminus v two is 0.250 meters per second. So a positive relative velocity means they are approaching each other. So we should rearrange our formulas here to get expressions v one minus v two because if we can make v one minus v two appear in our formula then we are on to something because we know what that difference is. So we're going to do a bit of work on the kinetic energy formula, the one halves cancel because we can multiply everything by two and then we'll collect the satellite one terms on the left side. So we'll subtract m one v one prime squared from both sides. We'll also subtract m two v two squared from both sides. So the m two terms disappear on the left and we have only m one terms there. So that's m one v one squared minus m one v one prime squared and there's a common factor m one now which we'll factor out here. So we have m one times v one squared minus v one prime squared on the left. Now on the right hand side the satellite one terms disappear and we're left with m two as a common factor between the two terms that remain and we'll factor that out, m two times v two prime squared minus v two squared. Oh, should be a squared there. There. Then this can be factored, this difference of squares could be instead written as v one minus v one prime times v one plus v one prime and likewise on the right hand side we're factoring the difference of squares and that's v one prime minus v two -- sorry, v two prime minus v two multiplied by v two prime plus v two. So whenever you have a squared minus b squared, you could factor it as a minus b times a plus b. Okay. So that's kind of nice because now we have this difference of velocities showing up which is good, but we need to do a bit more work on this and so we'll return to our momentum conservation formula and change how it looks. We can make a term that is the same as what shows up in our kinetic energy formula. So if we move this term to the left by subtracting it from both sides and then factoring out the m one, we get m one times v one minus v one prime. Likewise this term gets moved over to the right by subtracting it from both sides and we have a common factor m two multiplied by v two prime minus v two. Well since these two things are equal let's give it a name X, doesn't really matter what we call it, could have called it triangle or anything and we can substitute now for this and call it this thing. Let's call it X and it's multiplied by v one plus v one prime and then that equals the same thing because we're told that they're equal, let's call it X, multiplied by v two prime plus v two. Then divide both sides by this thing, whatever it is we don't care what it is because bye bye, it goes away, after we cancel it from both sides. So we're left with v one plus v one prime equals v two prime plus v two. Then we can rearrange this by moving these terms around and we have v one minus v two equals v two prime minus v one prime. So this is money because we know what v one minus v two is. It's 0.25 meters per second. So we're just going to do a bit of clean up stuff here, we're going to going to move the order of these two around by multiplying by negative one over -- multiplying by negative one twice I guess you could say So we can put a negative sign here outside of some brackets and then switch the orders around and this doesn't change the quantity, it just change the way it looks. So we have negative times v one prime minus v two prime -- yeah, how can I explain? I mean it's kind of one of these things that sort of simple and being simple makes it hard to explain. How do we make this negative show up there? It's kind of like multiplying this by negative one twice. So multiplying by negative one squared of course changes nothing because negative one times negative one is positive one and we can multiply anything we want by positive one. So let's multiply by negative one first one time which makes v two prime become negative and it makes the minus v one prime term become positive and then we're left with this second negative one leftover here. So there's the explanation. Okay. So now, we have -- well, the question is asking us what is the relative velocity after the collision and so I wanted to have v one prime minus v two prime in our final answer because that's what we're trying to find. So that's going to equal, well multiply both sides by negative one again, and we end up with this being positive and move it over to the left. Then on the right hand side we have negative v one minus v two. We know v one minus v two is 0.25 as we started with up here. We plug that in for this and so v one prime minus v two prime are going to be the negative of that, negative 0.250 meters per second. So after collision, the relative velocity will be of the same magnitude but in opposite direction so they're going to be receding from each other with a velocity of negative 0.250 meters per second.
Comments
Where is the calculator screenshot?
Hey Shaun you can explain the double multiplication of negative 1 that you were having a little difficulty with putting in simple terms as simply factoring the negative out of the two terms and thereby switching the signs of the values. One just needs to make sure that FOIL checks out when refactoring the negative back into the brackets.


