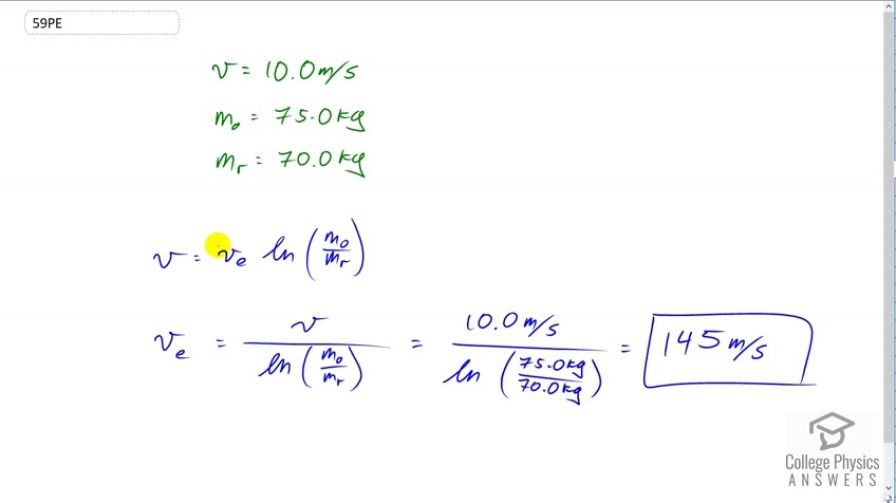
Given the following data for a fire extinguisher-toy wagon rocket experiment, calculate the average exhaust velocity of the gases expelled from the extinguisher. Starting from rest, the final velocity is 10.0 m/s. The total mass is initially 75.0 kg and is 70.0 kg after the extinguisher is fired.

Video Transcript

This is College Physics Answers with Shaun Dychko. This is our approximation for the final velocity of some rocket propelled thing, be it a toy wagon or an actual rocket, based on the exhaust velocity of the propellant, multiplied by the natural logarithm of its original mass divided by the mas that remains after shooting out the propellant. So we'll rearrange this to solve for the exhaust velocity and we'll divide both sides by the natural logarithm of m naught over m r, and switch the sides around and we get the velocity of the exhaust is the final velocity of the wagon divided by the natural logarithm of m naught over m r. So that's ten meters per second divided by the natural logarithm of 75 kilograms divided by 70 kilograms, giving us an exhaust velocity of 145 meters per second.