Question
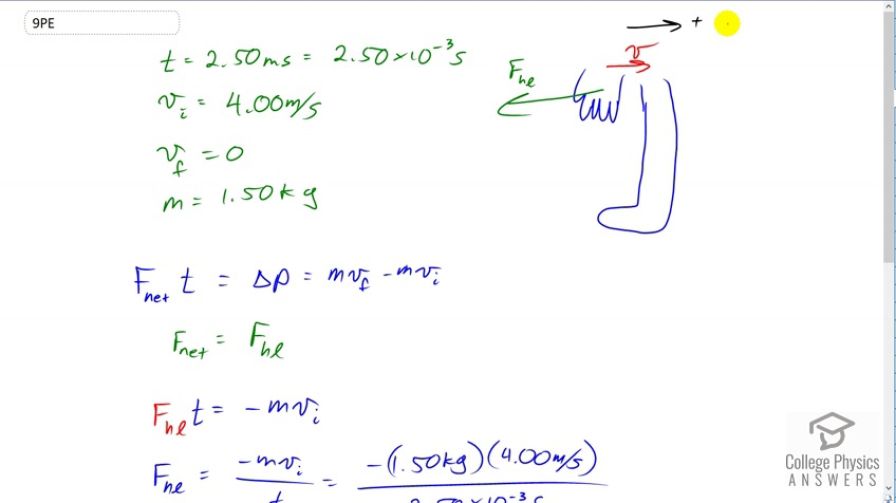
A person slaps her leg with her hand, bringing her hand to rest in 2.50 milliseconds from an initial speed of 4.00 m/s. (a) What is the average force exerted on the leg, taking the effective mass of the hand and forearm to be 1.50 kg? (b) Would the force be any different if the woman clapped her hands together at the same speed and brought them to rest in the same time? Explain why or why not.
Final Answer
a)
b) The same, since and are the same.
Solution video
OpenStax College Physics, Chapter 8, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This woman is bringing her hand to rest by slapping it against her leg and she is going to be moving it to the right in the positive direction. There is going to be a force exerted on the hand due to the leg and so I'll label that F subscript hl, force on the hand due to the leg because the question is asking what's the force on the leg due to the hand but we can't directly answer that because all we can do is talk about the hand itself. We're going to talk about the net force that the hand experiences multiplied by time. That's going to be the impulse or the change in momentum. Then after we figure out what this force is then we'll say well, it's the Newton’s Third Law counterpart to the force on the leg due to the hand. So we have the hand brought to rest within two and a half milliseconds converted into seconds. Initial speed in four meters per second and the hand and the forearm mass are 1.5 kilograms. So the net force times time is the mass times final velocity minus mass times initial velocity. Final velocity is zero so this just becomes negative m vi. The net force on the hand is the force on the hand due to the leg because there are no other horizontal forces. The gravity doesn't matter because it's perpendicular to the direction of motion here so it won't have any effect on things. So we have the force on the hand due to the leg multiplied by time substituted in for F net equals negative m times initial velocity. We'll divide both sides by time to get the force on the hand due to the leg is negative mass times initial velocity divided by time. So that's negative of 1.5 kilograms times four meters per second divided by 2.5 times ten to the minus three seconds which is negative 2.4 times ten to the three newtons. Now since the force on the leg due to the hand is the negative of the force on the hand due to the leg and that's true because of Newton’s Third Law, then that means the force on the leg due to the hand is 2.4 times ten to the three newtons positive which means it's towards the leg. In part B, if the woman was to clap her hands together instead of clapping her hand on her leg, each hand would experience the same magnitude force as we calculated in part A because the change in momenta and the change in time are the same. So, we get the force by going change in momentum divided by change in time and so if these numbers are the same, then the net force is going to be the same too.
