Question
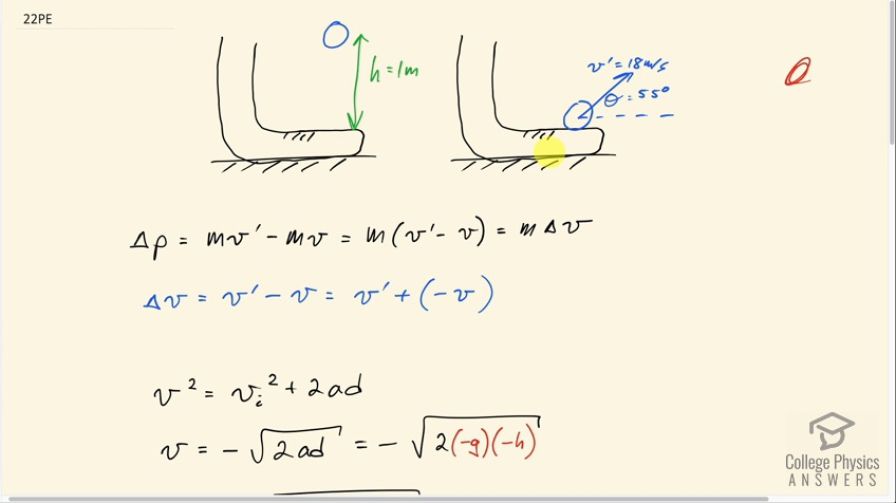
A punter drops a ball from rest vertically 1 meter down onto his foot. The ball leaves the foot with a speed of 18 m/s at an angle above the horizontal. What is the impulse delivered by the foot (magnitude and direction)?
Final Answer
, where is the mass of the ball in kilograms.
Solution video
OpenStax College Physics, Chapter 8, Problem 22 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
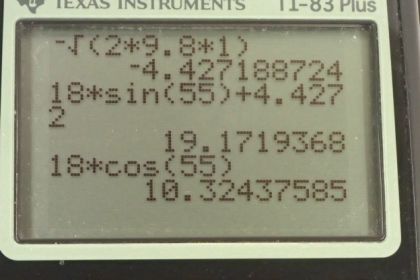
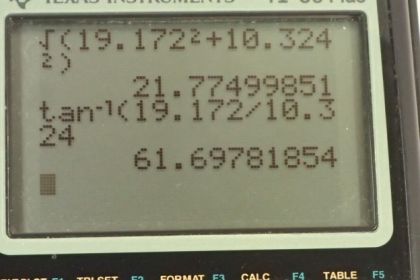
This is College Physics Answers with Shaun Dychko. This ball is going to fall 1 meter before it hits the punter's foot so punter is going to kick the ball and the foot's going to make the ball leave with a velocity of 18 meters per second at an angle of 55 degrees above horizontal and we are going to need to know what is the velocity of this ball when it reaches the person's foot. So as it falls this 1 meter, it will have some velocity here and we'll call that velocity v in this momentum equation so it has this velocity v here. So v is the velocity just before contacting the foot and v prime is the velocity after being kicked. So impulse is change in momentum and it's a vector quantity and we are going to have to take the difference between these final momentum and initial momentum as vectors. So we can factor out the m from each of these terms and so we have m times the change in velocity. So this is the final velocity v prime minus the initial velocity v. Okay! Now just for my own personal preference, I like to write vector differences, wherever there's a subtraction, I like to rewrite it as addition instead because I like to use the head to tail method for adding vectors all the time and so I am going to flip the second vector around by putting a minus sign directly in front of it and we are gonna add these vectors. So I am gonna rewrite v prime minus v as v prime plus negative v; it makes no difference to our result but I think it's just easier for me. So this vector v which is shown here is going to be now pointing upwards so this is negative v that's the opposite of v is— negative v— and that's the vector we are going to use in this addition. Okay! So to figure out what this velocity will be, we know that the velocity squared equals initial velocity squared plus 2 times acceleration times displacement; the initial velocity is zero because it's dropped from this initial height so it's not imparted any initial velocity at all so this term disappears and we are left with v after you take the square root of both sides is gonna be square root of 2ad and when you take the square root of both sides, you can choose the plus or the minus or both depending on your physical context and so in this context, because we can see that the velocity, just before hitting the punter's foot, is downwards that's gonna be the negative direction, or you know by convention defining 'up' and 'to the right' as positive, so we can choose the negative of this square root here. So we have the velocity just before hitting the person's foot is negative square root 2ad. Now acceleration is that due to gravity, g, but in the downward direction so negative g and then the displacement is negative this height h, negative 1 meter. Okay! So then we plug in numbers and we get that the speed just before hitting the person's foot is negative square root 2 times 9.8 meters per second squared times 1 meter which is negative 4.4272 meters per second. Now negative v is what we are interested in because that's what I'm gonna plug in here and that's negative of this answer which is positive 4.4272 meters per second and we expected that because we can see from this picture that the opposite of this vector downward is this vector up so negative v is indeed positive. Okay! So we add these vectors together now so now we are finally doing this so we are finding this change in velocity; it's gonna be v prime plus negative v. So this is v prime drawn here, 18 meters per second 55 degrees above horizontal— I've drawn that vector here— and then add to that with the tail of the second vector on the head of the first the negative v, which is positive 4.4272 meters per second, and then the resultant goes from the tail of the first vector to the head of the last vector so this is Δv in red that we are trying to find. So it's going to have a y-component and it's gonna be the sum of the y-component's of these two vectors. So the y-component of v prime is going to be this bit here in this right triangle. So here is v prime y-component and it's the opposite leg of this triangle and that means we need to use the sin function multiplied by the hypotenuse to find this opposite leg and that's what I have written here and then the y-component of this vector is the vector itself because it's entirely in the y-direction. So we have 18 meters per second times sin 55 plus 4.4272 meters per second giving 19.172 meters per second is the y-component of the change in velocity. And then for the x-component, we have the x-component of v prime and then add to that the x-component of negative v which is zero though because this vector does not go to the side at all. And so we have the x-component of the change in velocity then is 18 meters per second times cosine of 55— cos because this is the adjacent leg of this right triangle and we are multiplying cos of that angle by the hypotenuse— and that's 10.324 meters per second. And then we get the magnitude of the change in velocity by using Pythagoras theorem and so that's gonna be the square root of the square of each of the components added together and so that's square root of 10.324 meters per second squared plus 19.172 meters per second squared and square root that sum and you get 21.775 meters per second. And then this angle, which I'll call α, it's this angle here, it's gonna be the inverse tangent of this opposite leg which goes all the way from the beginning here to the very head of the resultant vector that opposite divided by the adjacent and then take the inverse tangent of that. So it's inverse tangent of the y-component divided by the x-component so that's the inverse tangent of 19.172 meters per second divided by 10.324 meters per second which is 61.698 degrees. So now we can say that our change in momentum or the impulse, in other words, is the mass of the ball which we are not given but we'll just have to say m in that case, multiplied by the change in velocity which is 22 meters per second when you round this to two significant figures multiplied by m—the mass of the ball— and at an angle of 62 degrees above horizontal.