Question
Military rifles have a mechanism for reducing the recoil forces of the gun on the person firing it. An internal part recoils over a relatively large distance and is stopped by damping mechanisms in the gun. The larger distance reduces the average force needed to stop the internal part. (a) Calculate the recoil velocity of a 1.00-kg plunger that directly interacts with a 0.0200-kg bullet fired at 600 m/s from the gun. (b) If this part is stopped over a distance of 20.0 cm, what average force is exerted upon it by the gun? (c) Compare this to the force exerted on the gun if the bullet is accelerated to its velocity in 10.0 ms (milliseconds).
Final Answer
- The plunger reduces the recoil force by 70%
Solution video
OpenStax College Physics, Chapter 8, Problem 14 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
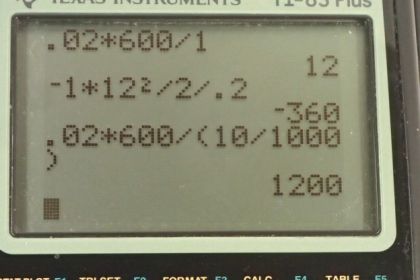
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The plunger inside the rifle is a mechanism that will reduce the recoil force experienced by the soldier holding the rifle. And the mass of this plunger is 1.00 kilogram; the mass of the bullet being fired is 0.0200 kilograms and the final velocity of the bullet, which is labeled 'prime' for final, is 600 meters per second and the initial velocity is zero. So we know that the mass of the plunger plus the mass of the bullet initially equals the sum of their masses after the bullet is fired and that's going to be zero because initially, they are both at rest. And this means the momentum of the plunger after the bullet is fired is the same as the momentum of the bullet after it's fired and I suppose you could have a negative sign here which would just indicate that the direction of a plunger is opposite to that of the bullet; the bullet goes forwards and the plunger goes backwards. So the plunger is kinda like the piece between the bullet and the soldier. Okay! So substituting mass times velocity in place of the plunger and bullet momenta and then divide both sides by m P and we get that the final velocity of the plunger is the mass of the bullet times the bullet's velocity after firing divided by the mass of the plunger. And that's 0.0200 kilograms times 600 meters per second divided by 1.00 kilogram which is 12.0 meters per second. Now in part (b), we are asked if the plunger is stopped in a distance of 20 centimeters, what average force is exerted upon it? So we know that the net force on it equals its mass times its acceleration and the net force will be this one force exerted by the gun and the soldier on the plunger so we need to figure out what this acceleration then is. So from our kinematics chapters, we know that the final velocity squared is initial velocity squared plus 2 times acceleration times displacement and the final velocity is zero because the plunger will come to a stop and then we can rearrange this to solve for acceleration. We'll subtract v initial squared from both sides and then divide both sides by 2d and we get acceleration then is negative initial velocity squared divided by 2 times displacement. So we can substitute that in place of the letter a here in this net force formula and we have then the net force on the plunger is mass times negative of the initial velocity squared divided by 2 times displacement. So that's negative of 1 kilogram times 12.0 meters per second squared divided by 2 times this displacement of 20 centimeters converted into meters by multiplying by 1 meter for every 100 centimeters and we get negative 360 newtons. Now in part (c), we are asked to compare this force that's on the plunger versus the force that was exerted on the bullet. So the force on the bullet multiplied by the time that that force is applied equals the impulse on the bullet and we know that the bullet is accelerated in a time of only 10 milliseconds so we can divide both sides by t to solve for the force on it. So that's gonna be its impulse divided by the time and the initial momentum is zero here— the bullet starts at rest—and so we have for the impulse then is 0.0200 kilograms times 600 meters per second divided by 10.0 milliseconds converted into seconds by multiplying by 1 second for every 1000 milliseconds and we are left with 1200 newtons. So the percent difference that this plunger mechanism made in the recoil force then is the difference between the force on the bullet versus the force on the plunger divided by the force on the bullet times 100 percent. So that's 1200 newtons minus 360 newtons divided by 1200 newtons times 100 percent which is 70 percent. So the plunger reduces the recoil force by 70 percent. So instead of the solider having to applying 1200 newtons, they instead apply 360 newtons due to this plunger mechanism that moves over a large distance of 20 centimeters inside the gun.