Question
Ernest Rutherford (the first New Zealander to be awarded the Nobel Prize in Chemistry) demonstrated that nuclei were very small and dense by scattering helium-4 nuclei from gold-197 nuclei . The energy of the incoming helium nucleus was , and the masses of the helium and gold nuclei were and , respectively (note that their mass ratio is 4 to 197). (a) If a helium nucleus scatters to an angle of during an elastic collision with a gold nucleus, calculate the helium nucleus’s final speed and the final velocity (magnitude and direction) of the gold nucleus. (b) What is the final kinetic energy of the helium nucleus?
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 49 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
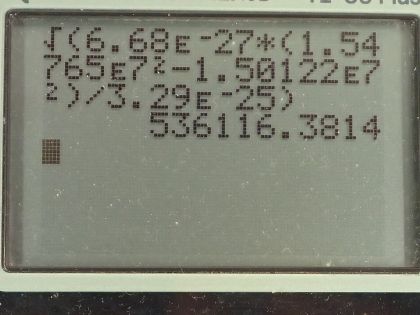
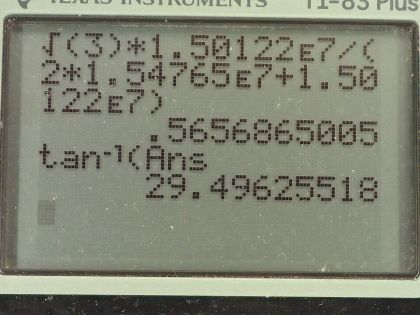
This is College Physics Answers with Shaun Dychko. This question is based on the Ernest-Rutherford experiment that demonstrated that the nucleus of an atom is small and dense. So it shows that it's small because this incoming helium nucleus would not get deflected very much most of the time... most of the time, it would miss the gold nucleus and zip on past maybe without getting deflected or maybe just getting deflected a tiny bit and so on but every once in a while, a helium nucleus would hit the gold nucleus dead on and have a dramatic reflection... have a dramatic change in its momentum and so the infrequency of this occurrence shows that the nucleus of the gold atom is small because not very many of these incoming helium nuclei would hit the nucleus of the gold atom and then also it shows that the gold nucleus is dense because there's so much mass in that tiny space enough to cause such a dramatic change in momentum of the helium nucleus. Okay! So we make some assumptions about what the incoming kinetic energy of the helium nucleus is— we are told that it's 8.00 times 10 to the minus 13 joules— we are given the mass of the helium nucleus and the mass of the gold nucleus abbreviation for gold is Au for some reason... I should probably look that up but it doesn't make sense really because it's not to do with the word 'gold'... probably Latin or something like that... just like 'iron' has an abbreviation Fe. So we have the masses and the kinetic energy of the helium nucleus and the angle of deflection. So it deflects at an angle of 120 degrees with respect to its direction of its initial velocity so it's being deflected somewhat backwards and up. Okay! After the impact—so this is the after picture here by the way— after the impact, we have the gold nucleus also moving recoiling due to the impact and it's going to have some speed v Au and some angle θ Au below the positive x-axis. Initially, the gold nucleus is stationary and that's all we need to know to figure out the speed of the helium nucleus after impact anything after impact is denoted with a prime so that's v He prime is to say the speed of the helium nucleus after collision... there's a little ' here too but it's kind of hard to see... maybe if I move it like this, you will see it... I didn't catch it... this is v Au prime here and we want to find out the angle of the velocity of the gold nucleus after impact as well as its speed. So in other words, the velocity of the gold nucleus after impact is one question which consists of two pieces of information— its direction and speed— and since we are given the direction of the helium nucleus after impact, we need to find only its speed. Okay! Momentum is conserved, which is to say the total momentum initially before impact equals the total momentum final after impact and this is true independently in the x and y-directions. So let's consider the x-direction. We will take the total momentum in the x-direction on one side initially and then we have the total momentum in the x-direction on the right hand side after impact. So initially, there is no momentum for the gold nucleus and so we have only the momentum of the helium nucleus but since we have chosen our x-axis to be along the initial direction of the helium nucleus that means all of its momentum is in the x-direction so there's no trigonometry needed to figure this part out. So this is mass of the helium nucleus times the speed of the helium nucleus on the left— that is the total momentum of the system. On the right hand side, we have the helium nucleus going in to the left in the x-direction and so we have a negative sign here to indicate that. I prefer to put negative signs explicitly in the formulas like this— it makes more sense to me— and I am going to use reference angles in the trigonometry so that we always get a positive answer to our, you know, cos of the angle or sin of the angle. So I'll use 60 degrees here, which is 180 minus 120. Okay! So if you had chosen to use cosine of 120 and had a plus here and that would be fine, you would end up with a negative as well. Okay! So add to that the mass of the gold nucleus plus the x-component of the gold nucleus velocity after impact. Okay! So we have negative mass of the helium times speed of the helium after impact times cosine of this reference angle— 180—minus the angle of recoil of the helium nucleus and add to that the x-component of the gold's nucleus momentum after impact And so we use cosine of this angle here because this is the adjacent leg of this triangle here so this is the momentum for the gold nucleus after impact and it has an x-component here and a y-component here this is v Au prime x component and v Au prime y component. Okay! And the x-component is to the right so it's positive and that's why there's a plus sign there. Alright! I am going to replace the 180 minus θ He I am going to replace it with 180 minus 120; now normally, I don't substitute for variables until the very end after doing a bit of algebra and that's usually a good idea but it just works out more nicely and saves us some writing to substitute for just this one number right now so I am going to plug in 120 for the recoil angle of the helium nucleus. And this makes cosine of 60 and cosine of 60 is a special answer because you should it's worth committing this triangle to memory... this triangle has sides of 1, hypotenuse 2 and this leg is root 3 provided this angle is 30 and this angle is 60 and this is a right angle here. And from this picture, we can see that the cosine of 60 is one-half— adjacent divided by hypotenuse— so this whole thing can be replaced by one-half and that's what I have done here... that's why it's divide by 2 because I am multiplying by a half here and otherwise, this line is unchanged. Okay! This is equation (1) that's as much as we can do in our consideration of the x-direction because at this point, we don't know the speed of the helium nucleus after collision and we also don't know the speed of the gold nucleus after collision nor do we know the angle of the gold nucleus after collision so we have one equation and three unknowns. That indicates that we need to have a total of three equations because you need as many simultaneous equations as you have unknowns in order to solve. So our second equation is going to come from the y-direction and initially, we have no momentum in the y-direction because only this helium nucleus has momentum initially and it is moving entirely in the x-direction. So we have 0 on the left and on the right hand side, we have the momentum of the helium nucleus in the y-direction minus the momentum of the gold nucleus in the y-direction and I put a minus here because I can see that this component is directed downwards for the gold nucleus and I am going to use this positive reference angle in here and I have to explicitly put in a negative sign to indicate this direction. Okay! And that's 180 minus 120 we will do the same business as we did up here replace that with this exact answer sin of 60 is root 3 over 2 and so replacing sin of 60, which is 180 minus 120, with root 3 over 2. And so we have equation number (2) which is that 0—initial y-momentum— equals root 3 over 2 times mass of the helium times the speed of the helium nucleus after impact minus mass of the gold nucleus times speed of the gold nucleus after impact times sin of the angle of the velocity of the gold nucleus. That's two equations, we have number (1) and number (2) and number (3) comes from the fact that the collision is elastic, which is to say that the kinetic energy is conserved during the collision. So the total kinetic energy, we have initially, is one-half times mass of the helium times speed of the helium squared and then after impact, we have one-half mass of the helium times speed of the helium after impact squared plus one-half mass of the gold times speed of the gold after impact squared and we will multiply everything by 2 to get rid of that pesky half that is unnecessary and we end up with equation number (3). Okay! So now comes algebra trickery! We need to figure out a way to solve these three equations and they look very different and you know one of our unknowns is buried inside a trig function and it looks messy. So one trick we can employ is to notice that we have a factor here and a factor here which are the same apart from the fact that one uses sin and the other uses cosine; they have the same coefficients— m Auv Au prime— and they have the same argument—θ Au— and the only difference is one is sin and the other is cosine and so that should make you think of this trigonometric identity which says that sin θ squared plus cos θ squared equals 1— that's a very useful trig identity. And so we are going to rearrange these two equations— we will call it version (b) so equation (1b) and equation (2b)— we are going to rearrange them such that we have this term on its own on one side and then we will square both equations, add them together and then the coefficients will factor out and we will be left with sin squared plus cos squared equaling 1. Alright let's see that in action! So equation (1b) is this one here where I have moved this term to the other side by adding it to both sides and then switch the sides around. So we have m Auv Au primecos θ Au on the left equals m Hev He plus m Hev He prime over 2. And then equation (2b) is going to take this term to the left side and so we have m Auv Au prime sin θ Au equals root 3 m Hev He prime over 2. There... that's useful because once we square equation (1b) and rewrite it here and I mean this is a binomial and we are going to square it and so we have the first term squared and then the cross-term is this one multiplied by the other one and then multiplied by 2 and then the last term is the second term squared. I mean I could do it all but I don't want to waste your time but yeah. So anyway this is of the form a plus b equals a squared plus 2ab plus b squared, where a is m Hev He and b is m Hev He prime over 2 so confirm that this works out to this line here. Alright! And equation (2b) squared is, you know, this— that part's straightforward because every little factor gets squared— and then the root 3 becomes 3 and then the denominator 2 becomes 4. Okay and here's the magic: we add these equations together so we add the left side together and we add the right side together. So adding the left sides together recognizing that these are common factors between the two terms that will result... I have already factored it out. So we have m Au squared times v Au prime squared times what's left which is cos squared θ Au plus sin squared θ Au and this equals m He squared, which is a common factor between every single term here so I factored it out and then we have what's left over after dividing every term by m He squared which is v He squared plus v Hev He prime— that's from this term— plus v He prime squared over 4— that's this term here— and then we have 3 v He prime squared over 4. These two terms have common denominator and they can be collected together and so we end up with v He prime squared and then this becomes 1 and that's awesome because that eliminates that variable from our equation— we no longer have a θ Au in the way— and we are one-step closer to being able to solve this equation— we'll call this equation number (4). (Oh sorry) I wrote a 0 there... that's not a 0 that's a 1... that's important so we are multiplying by 1 here that's what cos squared θ Au plus sin squared θ Au is. Alright! We still have two unknowns so we need to use a third equation to get rid of yet another unknown so that we have only one unknown left. We are going to replace v Au prime squared and we can do that using equation (3) because if we move this to the left side and then divide both sides by m Au, we isolate v Au prime squared and so that's what I did here. And then we can substitute this in place of v Au prime squared in equation (4) and that is what we are doing in this line here. So this is equation (4) rewritten but instead in red, I have replaced v Au prime squared with all of this. Okay! And then we'll multiply through by m Au and so this is m Au to the power of 1 after canceling with the denominator there and we have m Aum Hev He squared minus m Aum Hev He prime squared equals on the right hand side all of this and that's just multiplying through by m He squared into each term so that got distributed into the brackets. And then we have an equation with only one unknown— which is v He prime— it's a bit messy because it is squared in one term and then it's to the power of 1 in another term and then it doesn't exist at all in the third term and that means it's a quadratic equation and we can use our quadratic formula to solve it. By the way we can figure out v He because since we are given the initial kinetic energy of the helium nucleus, we can solve this to determine what the initial speed of the helium nucleus was. So we have one-half m Hev He squared— this is the initial kinetic energy— and we are told that it's 8.00 times 10 to the minus 13 joules and we will multiply both sides by 2 over m He and we end up with v He after taking the square root of both sides equals the square root of 2 times 8.00 times 10 to the minus 13 joules divided by the mass of helium, which is 6.68 times 10 to the minus 27 kilograms and that's 1.54765 times 10 to the 7 meters per second. So this equation is of the form a times some unknown squared plus b times that same unknown plus some constant term c equals 0 and so that means quadratic formula to the rescue. So v He prime will be the negative of the coefficient of the linear term plus or minus this square root of the linear terms coefficient squared minus 4 times the coefficient of the quadratic term times the constant term divided by 2 times the coefficient of the quadratic term. Anyway... we have to figure out what each of these coefficients are now. So the coefficient a is m He squared plus m Au times m He— that's what is written here— that's the coefficient of the squared term and that's 6.68 times 10 to the minus 27 kilograms squared plus 3.29 times 10 to the minus 25 kilograms times 6.68 times 10 to the minus 27 kilograms and this works out to 2.24234 times 10 to the minus 51. I didn't write units here... normally, I do but the units are weird this works out to, well... just for curiosity, it's kilograms squared... it's kind of meaningless though each of these terms needs to have kilograms squared meters squared per second squared as their units but the coefficients are going to have different units for each term. Okay! So the coefficients are going to have different units because they are being multiplied by different powers of the unknown. Okay! The coefficient b—the coefficient of the linear term, which is the unknown to the power of 1— is m He squared times v He and so that is 6.68 times 10 to the minus 27 kilograms squared times 1.54765 times 10 to the 7 meters per second and that is 6.90599 times 10 to the minus 46 kilograms squared meters per second. c—the constant term—is all this stuff here which is m Hev He squared times m He minus m Au. So this works out to 6.68 times 10 to the minus 27 kilograms times 1.54765 times 10 to the 7 meters per second squared times the difference in masses of the helium and gold nuclei, this is negative 5.15714 times 10 to the minus 37 and that's kilograms squared meters squared per second squared. Okay! So the speed of the helium nucleus after collision is the negative of the coefficient of the linear term so negative of this number plus or minus the square root of that number squared minus 4 times the coefficient of the squared term and then times the constant term— and remembering to put that negative in there— divided by 2 times a so to speak and this works out to 1.50122 times 10 to the 7 meters per second. There we go... we have answered part of the question! And then the next part is to figure out what is the speed of the gold nucleus after collision? And so we can rearrange equation (3) or take the square root of both sides actually and we end up with solving for v Au prime and that's the square root of mass of helium nucleus times the speed of the helium nucleus initially squared minus the helium nucleus speed after collision squared divided by the mass of the gold nucleus so we plug in all of those numbers here and we end up with 5.36116 times 10 to the 5 meters per second. And that's two out of three questions answered... the third question for part (a) is the direction of the gold nucleus after collision. So to figure that out, we need to do some more trigonometric trickery using this identity here which is that the ratio of sin of an angle divided by cosine of that same angle equals tangent of the angle. And so when we divide equations (2b) by (1b) we end up having sin divided by cosine because these coefficients will cancel, these common factors will cancel and we are left with tangent on the left side here and on the right hand side, we have some stuff that we will clean up in a second so let's just look back at (2b) and (1b). So here's (1b)—it's this whole right hand side that we are concerned with here... this part here— and this is the denominator of the work that we are doing down there and the numerator is going to be this part here so we are going (2b) divided by (1b) so this is the numerator and that's what's written here and we are dividing by the right hand side of equation (1b) here. Okay! Let's multiply top and bottom here by 2 over mass of helium nucleus and this makes the denominator 2 there cancel and mass of helium cancels on the top leaving us with root 3 v He prime and on the bottom, the 2 cancels here and then 2 becomes the coefficient for v He and the mass of the helium cancels for both terms. And so we have tangent of the angle of the gold nucleus after collision is root 3 times the speed of the helium nucleus after collision divided by 2 times the initial speed of the helium nucleus plus the speed of the helium nucleus after collision. So that's root 3 times 1.50122 times 10 to the 7 meters per second divided by 2 times 1.54765 times 10 to the 7 meters per second plus the final speed of the helium nucleus and that is 0.565687. Now the angle is going to be the inverse tangent of that which is 29.496 degrees. Alright! So we can have three significant figures in our answers because the information we are given in the question has three significant figures. So the speed of the helium nucleus after collision is 1.50 times 10 to the 7 meters per second, the speed of the gold nucleus after collision is 5.36 times 10 to the 5 meters per second and its direction is 29.5 degrees below the positive x-axis and we can see that is the direction based on this diagram it must be going below the positive x-axis. Okay! We are not done yet though... hang on... there's a little bit at the end here for part (b): what is the final kinetic energy of the helium nucleus? So that's a straightforward calculation: one-half mass of the helium nucleus times its speed squared after the collision and that's one-half times 6.68 times 10 to the minus 27 kilograms times 1.50122 times 10 to the 7 meters per second squared, this works out to 7.53 times 10 to the minus 13 joules. So give yourself a pat on the back if you followed all of this, you are in great shape for doing the most complicated question you can possibly get I think in an algebraic physics course on momentum.
Comments
What happened to the cos(180-theta He in after you added 1b^2 and 2b^2?
What happened to the cos(theta HE) ?????
Hi I wonder, at 10:26, equation 4, shouldn't the 2 v He v Au be just v He v Au, since cos (180 - theta hellium) is 1/2 cancels the 2 in front of the term?
Astute observation! I have made corrections to the final answers after accounting for this error. Please see the notes in the final answer for more details, and thanks again for noticing this.
This video was updated on Dec. 21st, 2023.