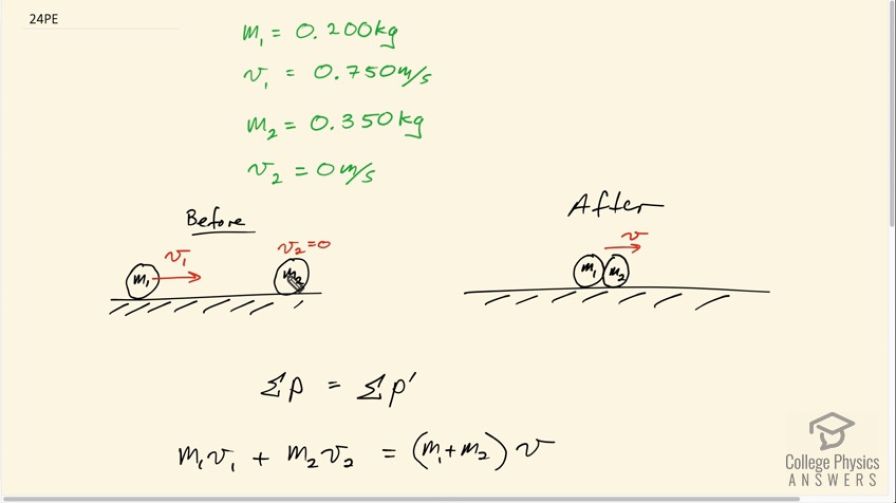
Suppose a clay model of a koala bear has a mass of 0.200 kg and slides on ice at a speed of 0.750 m/s. It runs into another clay model, which is initially motionless and has a mass of 0.350 kg. Both being soft clay, they naturally stick together. What is their final velocity?

Video Transcript

This is College Physics Answers with Shaun Dychko. The clay model of a koala bear of mass .2 kilograms is sliding towards an initially stationary clay model of mass .35 kilograms. And these two things are going to stick together. Because their made out of clay so they're sticky. So after collision, it becomes one single mass moving with some velocity, which we’ll call just v. Whereas before we had subscripts in our velocity v one and v two, before the collision in order to associate them with their respective masses. Okay, so the total momentum before the collision equals the total momentum after collision. And this prime symbol indicates that the thing is after. So we have m one times v one, that’s the momentum of mass one initially. Plus the momentum of mass two initially which is zero since there is no velocity initially. It’s going to equal the total mass of this single object which is m one plus m two, multiply by it’s common their common velocity of v. And so we’re going to, well, get rid of this term because v two is zero. And then switch the sides around, and we have m one minus m two, times v equals m one v one And then we divide both sides by the total mass here. And we’re left with v is m one v one over the total mass. So that’s .2 kilograms times .75 meters per second, divided by .2 plus .35 kilograms, which is 0.273 meters per second. So when they stick together, they move with a velocity of 0.273 meters per second.