Question
Confirm that the results of the example Example 8.7 do conserve momentum in both the x - and y -directions.
Final Answer
Please see the video solution.
Solution video
OpenStax College Physics, Chapter 8, Problem 46 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
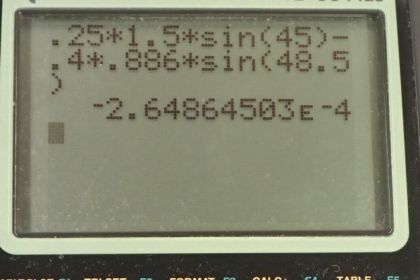
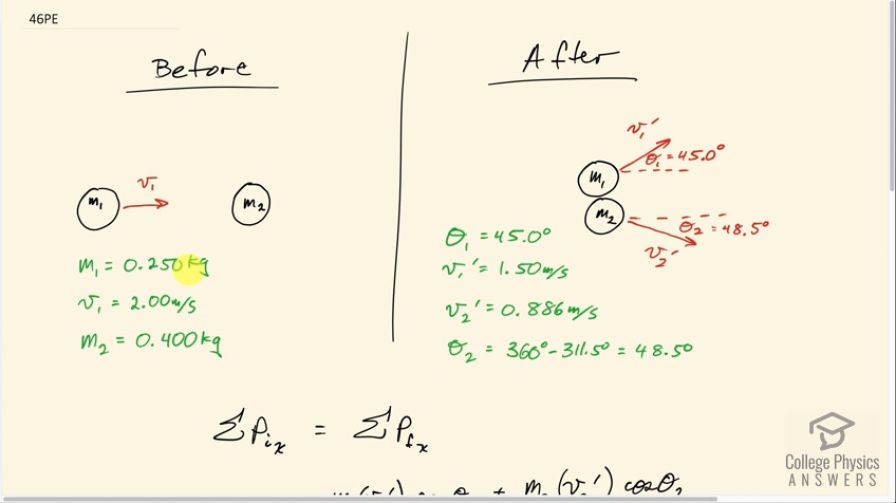
This is College Physics Answers with Shaun Dychko. In example 8.7, we were given a problem where this puck with mass 0.250 kilograms is moving on a frictionless surface and then impacts this mass m 2 which is initially stationary and then m 1 deflects at an angle of 45 degrees with some new velocity v 1 prime and m 2 is going to be given some velocity v 2 prime at some angle which turns out to be 48.5 degrees below horizontal. And v 2 prime is 0.886 meters per second and m 2 is 0.400 kilograms. And we are meant to take these results for v 2 prime and Θ 2 and confirm that momentum is conserved in the x-direction and in the y-direction. So our x-axis will be defined as the direction of the initial velocity of m 1 so we'll take that to be along the x-direction and then we'll take y to be positive upwards. And we'll check each axis independently so initially, we'll look at the x-axis and we'll say that the total momentum in the x-direction initially has to equal the final total momentum in the x-direction. So initially the momentum in the x-direction is m 1 times v 1 and there's no need for any trigonometry since this vector v 1 is... we are defining to be along the x-axis. After the collision, we are gonna take the component of this momentum along the x-direction and then add to that the component of the m 2's momentum in the x-direction. So the x-direction is the adjacent leg of this triangle here— if we imagine this triangle— we are gonna use cosine of Θ 1 multiplied by m 1v 1 prime will give us the x-component of the momentum of mass 1 and then cos of Θ 2 times m 2v 2 prime will give us the x-component of the momentum of mass 2. So we'll plug in the numbers and then confirm that the left side equals the right side and if that's true that is to say momentum is conserved because the total you had to begin with is the same as the total after collision. So 0.25 kilograms times 2 meters per second is 0.50 kilogram meters per second; that's the left side and on the right hand side, we have 0.25 kilograms times 1.50 meters per second because this m 1 slows down from 2.00 to 1.50 meters per second and we multiply that by cos 45 and then add to that 0.400 kilograms—mass 2— times 0.886 meters per second times cos of 48.5 degrees and that indeed does give 0.50 kilogram meters per second total momentum after collision so momentum is conserved in the x-direction. In the y-direction, there is no momentum initially because this thing is not moving up or down, it's moving only to the right along the x-axis and so after the collision, we expect the total momentum to also be zero. So we have this... m 1 is moving in the positive y-direction and mass 2 has a momentum in the negative y-direction. So I put a minus here to indicate that the momentum for mass 2 is downwards and in the negative direction. So we have m 1v 1 prime times sin of Θ 1— that's the momentum of mass 1 in the y-direction— minus m 2v 2 prime sin Θ 2; we'll see if that equals zero. So we have 0.250 times 1.50 meters per second times sin 45 minus 0.400 kilograms times 0.886 meters per second times sin 48.5 and that gives negative 2.6 times 10 to the minus 4; this is close enough to zero that we can say: yes, they are the same, they are both zero. This number is rounded and this number is rounded... I would imagine if we had more decimals in these numbers, we would probably get this closer to zero still.