Question
A battleship that is and is originally at rest fires a 1100-kg artillery shell horizontally with a velocity of 575 m/s. (a) If the shell is fired straight aft (toward the rear of the ship), there will be negligible friction opposing the ship’s recoil. Calculate its recoil velocity. (b) Calculate the increase in internal kinetic energy (that is, for the ship and the shell). This energy is less than the energy released by the gun powder—significant heat transfer occurs.
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 34 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
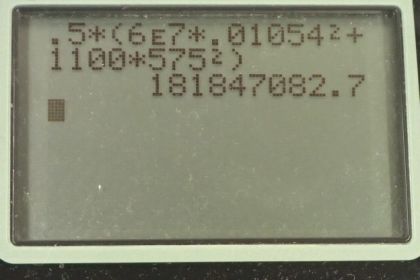
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A battleship with mass 6 times 10 to the 7 kilograms is initially at rest before this shell is fired. The shell is also here inside the barrel of the gun and after it's fired out, it's gonna have some speed to the left say and then the battleship will have some recoil to the right so that the total momenta of the battleship artillery shell system will be the same after the shell was fired as it was initially. So the momentum initially is going to be zero because neither of these things are moving so we have that the momentum of the battleship which we label with the number 1 plus the momentum of the shell which we label with number 2 initially is going to equal the total momenta after firing—that's what the prime denotes is to say that this is after the shell's been fired— and this total has to be zero since there was no movement initially so no momentum initially in other words. Okay! So we are gonna solve for this v 1 prime this speed of the battleship after the artillery firing and so we can solve for P 1 prime by moving this to the right hand side, or subtracting it from both sides you could say and we have P 1 prime equals negative P 2 prime; this negative sign means that the momenta are in opposite directions. Then we substitute for the momentum with our formula, mass times velocity, so P 1 prime then is m 1 times v 1 prime and P 2 prime is m 2v 2 prime and we can solve for v 1 prime by dividing both sides by m 1 and we get that the speed of the battleship then is negative m 2v 2 prime over m 1. So that's negative of the mass of the artillery shell which is 1100 kilograms times its velocity which is negative 575 meters per second divided by the mass of the battleship which is 6.00 times 10 to the 7 kilograms which gives a speed of 0.011 meters per second. And strictly speaking I guess, this is a velocity and the positive indicates that it's to the right hand side where we have a coordinate system with 'to the right' being positive. Because I put this left... velocity v 2 prime, I put that in as negative here. Okay! So part (b) asks us what is the change in kinetic energy as a result of fire in the artillery shell? So that's gonna be the total final kinetic energy minus the total initial kinetic energy; there is no initial kinetic energy because the shell and the ship are not moving and so this change in kinetic energy is going to be the final kinetic energy of both things: the battleship and the shell. So there's a factor one-half that we factor out from each of these kinetic energy formulas and we have this one-half times then m 1—mass of the battleship— times its speed after firing squared plus the mass of the artillery shell multiplied by its speed after firing squared. So we have one-half times 6.00 times 10 to the 7 kilograms times 0.01054 meters per second squared plus 1100 kilograms times 575 meters per second squared giving 1.8 times 10 to the 8 joules.