Question
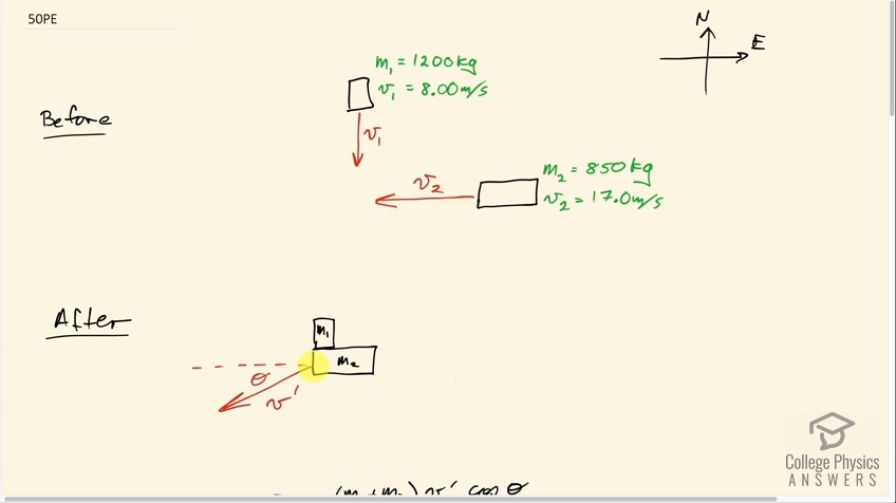
Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1200 kg and is approaching at 8.00 m/s due south. The second car has a mass of 850 kg and is approaching at 17.0 m/s due west.
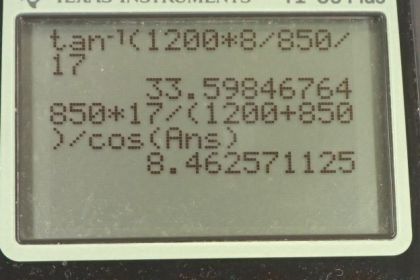
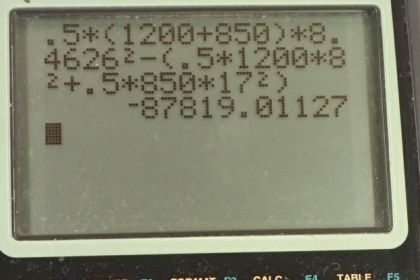
(a) Calculate the final velocity (magnitude and direction) of the cars. (b) How much kinetic energy is lost in the collision? (This energy goes into deformation of the cars.) Note that because both cars have an initial velocity, you cannot use the equations for conservation of momentum along the x -axis
and y -axis; instead, you must look for other simplifying
aspects.
Final Answer
- of kinetic energy was lost.
Note that the question's claim that momentum is not conserved along the x and y axes is nonsense.
Solution video
OpenStax College Physics, Chapter 8, Problem 50 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. These cars are approaching this icy intersection and then when they collide, they will stick together and slide off with some velocity v prime at some angle Θ below the horizontal. So car, we'll it number 2, has mass 850 kilograms and it's going due west at a speed of 17.0 meters per second and car 1 is going due south at 8.00 meters per second and it has a mass of 1200 kilograms. So this is an inelastic collision in which they stick together and we'll consider each of the axis independently. In the x-direction, we can say that the total initial momentum which is just that of car 2, m 2v 2, equals the momentum in the x-direction after they stick together which is gonna be m 1 plus m 2 stuck together times v prime times cosine of Θ because this is the velocity triangle but you could also say that it's the momentum triangle because this vector is in the same direction as the momentum would be. And so this leg here is the adjacent leg of this right triangle and we can use cos to find it therefore. So and I also I guess have positive to the left here and positive down by the looks of it. Okay! So in the y-direction, we have m 1v 1 is the total momentum in the y-direction initially because car 2 has no momentum in the y-direction at all and then after collision, we have m 1 plus m 2 times v prime times sin of Θ because it's this opposite leg here that we are interested in for the y-direction after the collision and so we multiply by sin of Θ to get that opposite leg of this right triangle. So we have two equations and two things that we don't know: v prime and Θ and so we need to do some algebra to combine these equations to solve for the unknowns. So what I'm gonna do is take the right hand sides and switch them around and then divide them so that we have m 1 plus m 2 v prime sin Θ divided m 1 plus m 2 v prime cos Θ and so that's what I have written here— I don't need the subscript '1' there— and doing this is strategic because the v prime's will cancel and so will some of the masses and we'll be left with sin Θ divided by cos Θ which has a trigonometric identity of tangent Θ and that will equal the other sides divided so that's m 1v 1 divided by m 2v 2. So tan Θ is m 1v 1 over m 2v 2 and then we can take the inverse tangent of both sides to solve for Θ. So Θ is the inverse tan of m 1v 1 over m 2v 2. So that's the inverse tangent of 1200 kilograms times 8.00 meters per second divided by 850 kilograms times 17.0 meters per second which is 33.6 degrees. And then we'll figure out what v prime is and we can rearrange this formula to figure that out; it's gonna be m 1v 1 over the total mass times sin of Θ or actually, take this x-direction, just the same so divide this by m 1 plus m 2 times cos Θ divide this by m 1 plus m 2 times cos Θ and that will solve for v prime as well and that's actually what I ended up doing here. So v prime then is 850 kilograms times 17.0 meters per second divided by the total mass times cos of this angle we just found and that is 8.46 meters per second. And so the velocity after sticking together is 8.46 meters per second, 33.6 degrees south of west because this angle is towards the south compared to west. Okay. And then the next question is: how much kinetic energy was lost? And so we'll take the final kinetic energy and take away from that the initial kinetic energy. So the final kinetic energy is one-half times the total mass times this v prime squared and then from that we'll take the kinetic energy of car 1 when it's moving by itself and add to that the kinetic energy of car 2 when it's moving by itself initially. This works out to 8.78 times 10 to the 4 joules of kinetic energy was lost.