OpenStax College Physics, Chapter 8, Problem 40 (Problems & Exercises)

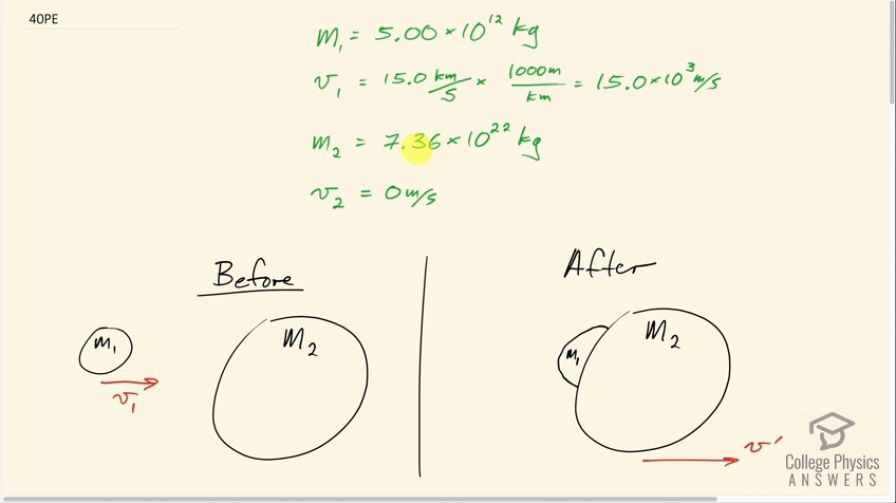
This is College Physics Answers with Shaun Dychko. A meteorite with a mass of 5 times 10 to the 12 kilograms is on a collision course with the Moon that has a mass of 7.36 times 10 to the 22 kilograms and the meteorite is approaching with a velocity of 15.0 times 10 to the 3 meters per second after we convert this kilometers per second into meters per second by multiplying by 1000 meters for every kilometer. So after the collision, which we assume is perfectly in elastic which is to say that the meteorite sticks to the Moon, this whole system of Moon and meteorite will together move with some velocity v prime and we have to figure out what that will be. So the total initial momentum of the system which consists only of the momentum of the meteorite equals the total momentum after collision. So initially we have a momentum of m 1v 1 and then after collision, we have the total mass of the meteorite plus Moon multiplied by its common velocity v prime and we'll solve for v prime by dividing both sides by m 1 plus m 2 so we have v prime is m 1v 1 over m 1 plus m 2. So that's 5.00 times 10 to the 12 kilograms— mass of the meteorite— times 15.0 times 10 to the 3 meters per second divided by the total mass and we get 1.02 times 10 to the minus 6 meters per second. So that's 1 micrometer per second; it's a very small velocity which we expect since the Moon is so much more massive than this meteorite. Part (b) asks us how much kinetic energy is lost after the collision? So the total final kinetic energy is one-half times the total mass of the Moon plus meteorite multiplied by v prime squared and then from that we'll take the initial kinetic energy when the meteorite is moving on its own which is one-half m 1v 1 squared. So that's one-half times total mass times the speed we calculated in part (a) squared minus one-half mass of the meteorite times its initial velocity squared and that gives 5.63 times 10 to the 20 joules of kinetic energy was lost. In part (c), we are told about a NASA experiment where they launched a rocket and intentionally collided it with the Moon and the rocket's mass was 2000 kilograms and its approach velocity was 2500 meters per second when we convert this 9000 kilometers per hour into meters per second by multiplying by 1 hour for every 3600 seconds and then multiplying by 1000 meters for every kilometer. And so the velocity after the inelastic collision will have the same formula as it did before but now instead of m 1v 1, we have m Rv R where it's the mass of the rocket now instead of the mass of the meteorite and this works out to 6.79 times 10 to the minus 17 meters per second and this is a much lower velocity despite a higher approach speed because the rocket is so much less massive than the meteorite was in part (a) and (b). And then we ask how much kinetic energy is lost and it's the same idea but just different numbers now, different mass for the mass of the rocket instead of the mass of the meteorite here and a different recoil velocity v prime now and we end up with 6.25 gigajoules of kinetic energy was lost.