Question
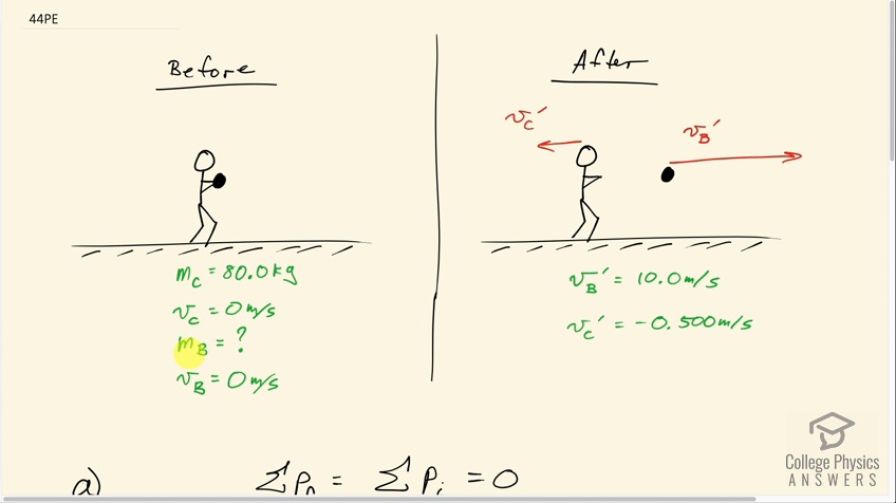
(a) During an ice skating performance, an initially motionless 80.0-kg clown throws a fake barbell away. The clown’s ice skates allow her to recoil frictionlessly. If the clown recoils with a velocity of 0.500 m/s and the barbell is thrown with a velocity of 10.0 m/s, what is the mass of the barbell? (b) How much kinetic energy is gained by this maneuver? (c) Where does the kinetic energy come from?
Final Answer
- The energy comes from food energy converted into kinetic energy by the clown's muscles.
Solution video
OpenStax College Physics, Chapter 8, Problem 44 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A clown on some frictionless ice skates is initially at rest and holding a barbell and the barbell has an unknown mass that we have to find in part (a); the clown's mass is 80.0 kilograms and the clown is going to throw the barbell with a velocity of 10.0 meters per second in one direction and the recoil velocity of the clown in the opposite direction will be 0.500 meters per second and have a negative sign to indicate it's to the left taking right to be the positive direction. And so we have that the total final momentum in this picture equals the total initial momentum in this picture which is zero because in this picture nothing is moving. So the mass of the clown multiplied by the recoil velocity of the clown plus the mass of the barbell multiplied by the velocity that the barbell is thrown all has to equal zero and we can solve for m B by subtracting m Cv C prime from both sides and then dividing both sides by v B prime. So we have that the mass of the barbell then is negative m Cv C prime over v B prime. So that's negative of 80 kilograms— mass of the clown— multiplied by negative 0.500 meters per second— clown velocity after the barbell is thrown— divided by 10.0 meters per second—velocity of the barbell after it's thrown— and that is 4.00 kilograms is the mass of the barbell. Part (b) asks us how much kinetic energy is gained by this maneuver of throwing the barbell. So it's going to be the difference between the total final kinetic energy and the total initial kinetic energy; there's no initial kinetic energy because there's no movement and so this change in kinetic energy will just be the kinetic energy of the barbell and clown after the barbell is thrown. So that's one-half mass of the clown times v C prime squared plus one-half m B times v B prime squared. So that's one-half 80.0 kilograms times 0.500 meters per second squared plus one-half times 4.00 kilograms— mass of the barbell—times 10.0 meters per second squared which is 210 joules. This energy comes from food energy that's been converted by the clown's muscles into kinetic energy.
