Question
A 70.0-kg ice hockey goalie, originally at rest, catches a 0.150-kg hockey puck slapped at him at a velocity of 35.0 m/ s. Suppose the goalie and the ice puck have an elastic collision and the puck is reflected back in the direction from which it came. What would their final velocities be in this case?
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 30 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
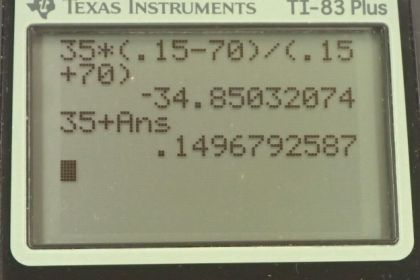
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. There is an elastic collision between a puck that’s initially moving with a velocity of 35 meters per second with a mass of .15 kilograms. And a goalie that's initially stationary, and the goalie mass is 70 kilograms. And the question is what will the velocities of the puck and goalie be after the collision? And with the extra piece of information is to say that it’s an elastic collision. So, we'll say that the total initial momentum has to equal the total final momentum is it always does. The total initial momentum is just that of the puck, since the goalie is initially at rest. So we have mass p times velocity p equals the final momentum, which is the mass of the goalie times velocity of the goalie prime, which is after collision. Plus mass of the puck, times velocity the puck prime. Now we can’t answer the question just with that one equation, because there are two things we don't know; the velocity of the puck after collision, and the velocity of the goalie after the collision. So because we have two unknowns, that means we need to have two equations to solve for them. Now this is the second piece of information that we know; that the kinetic energy will be conserved. That's what it means to say when you have elastic collision, is to say that the total final kinetic energy is the same as the total initial kinetic energy. No energy was turned into heat during the collision, or any other form. So, initially the only thing with kinetic energy is the puck. So we have, we’ll I guess I can put one half in front of all these, but the one half is gonna cancel anyway. So the initial kinetic energy is one half mass of the puck times velocity of the puck squared. And that equals the total final kinetic energy, which is one half mass of the goalie, times the goalie's velocity after collision squared. Plus one half mass of the puck, times velocity of the puck after collision squared. And then we're going to do some algebra in order to combine these two equations. It’s a little bit tricky because the unknown is squared in the second equation. Whereas it’s to the power of one in the first equation. So we're going to do some work on the second one, in order to write it in a way that has the unknown to the power of one. And we can do that when we, first of all let’s get rid of these half's everywhere, multiply both sides by two, and that's gone. we're going to do that by moving this term to the left side, which is to say subtracted from both sides. And we’re left with m p v p squared minus m p v p prime squared, and that equals this term leftover m g v g prime squared. And then the magic happens when we factor this difference of squares. So the first line here, I factored out the mass of the puck from both these two terms here. So m p times bracket v p squared minus v p prime squared. And then, this is a difference of squares which is pattern you need to be able to recognize. Whenever you see a squared minus b squared, you can instead write it as a minus b times a plus b. If doing so is helpful. And it is helpful for us, because it takes these variables that are squared and turns them into variables that are to the power of one. And now what’s going to happen next is that we can also write equation one, in a way that resembles what we're left here in equation two b. We can take this term to the left side in equation one. So, that leaves us with m p v p, minus m p v p prime equals this. And that's what I've written here. And then factor out the m p’s. So we have m p times v p minus v p prime, equals mass of the goalie, times velocity of the goalie after collision. Now, this whole thing here appears in equation two b. And we can substitute it with this, because this means zero, those two things are equal. So we write equation two again, but this time instead of m v p minus v p prime, we're writing m g v g prime in it’s place. And I’m doing my substitution in red here as usual, and then we carry on writing the rest of it. So multiplied by v p plus v p prime equals m g v g prime squared. Now, when you divide both sides by m g v g prime, you end up with this line here, which is to say that the velocity of the puck before collision, plus its velocity after the collision equals the velocity of the goalie after the collision. And this is a general result for elastic collisions, and some textbooks will say you know, remember this and just use that directly in your problem-solving. But instead I chose to basically derive it from this initial concept of kinetic energy being conserved here. So this is useful because we can then in-turn go back to equation one again. And I'm looking at equation one in its original form here, and we can replace the velocity of the goalie after collision. We can replace it with all this, and that's what's written in red here. There used to be a v g prime there, but not anymore. Now there's this, and now we have an equation with only one unknown. We’re given v p, the initial velocity of the puck. And we need to find v p prime, and it’s all to the power of one, which is good. And so the rest of this is just algebra to solve for v p prime. So we're going to distribute the m g into the brackets there, multiply both terms by mass of the goalie. And then collect the unknown term on the left. But, well, what happens is the only term that moves is this term, and so it gets subtracted from both sides. And so that's why there's a minus m g v p here. And then I switch the sides around, so that their unknown v p prime is on the left. So this term I got moved over here and then the sides gets switched around. And then factor out v p prime and you end up with v p prime, times m g plus m p on the left. And then divide both sides by that binomial. And we’re left with v p prime equals v p, which I also factored out on the right side times m p minus m g, divided by m p plus m g; So that’s 35 meters per second, times .5 kilograms minus 70 kilograms. Divided by .15 kilograms plus 70 kilograms, and this works out to negative 34.9 meters per second. The negative indicates that the puck is moving in the opposite direction after the collision compared to what it was initially. And the velocity of the goalie after the collision is, we can use this formula here, equation two version c. And say that it’s the sum of the velocities of the puck before and after the collision. So that’s 35 meters per seconds before, plus negative 34.8503 meters per second after collision. And that works out to positive 0.15 meters per second. And we expected a positive answer here because we have this goalie that was standing here initially at rest and a puck moving towards him, some initial velocity v p, and then the puck bounces off of him and it’s gonna push him away here. And so this is velocity of the goalie after collision, and then the puck has rebounded and it’s going backwards. There we go.