Question
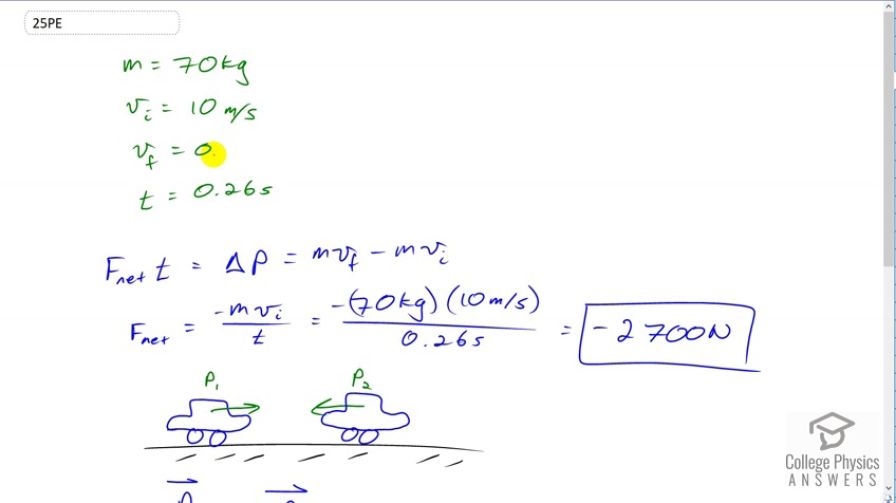
Consider the following question: A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate the force the seatbelt exerts on a passenger in the car to bring him to a halt. The mass of the passenger is 70 kg. Would the answer to this question be different if the car with the 70-kg passenger had collided with a car that has a mass equal to and is traveling in the opposite direction and at the same speed? Explain your answer.
Final Answer
We don't know how quickly the passenger will stop, so we can't calculate the force.
Solution video
OpenStax College Physics, Chapter 8, Problem 25 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A passenger of mass 70 kilograms is in a car that collides with a tree and they're initially going at ten meters per second and then the tree brings the car to a stop in a time of 0.26 seconds. The question is what force does the seat belt exert on the passenger while bringing them to a stop. So the impulse which is that net force which is going to be the force of the seat belt since there'll be only one horizontal force, multiplied by time is the impulse which is the change in momentum, so that's m v f minus m v i. The final velocity is zero and so this reduces to negative mass times initial velocity. So we'll divide both sides by t to solve for F net and so the force that the passenger experiences is the negative of their mass times their initial velocity, divided by time. So it's negative 70 kilograms time ten meters per second, divided by 0.26 seconds which is negative two thousand seven hundred newtons. Now, we're asked to compare that with a case where the car collides with a different car instead of a tree and this other car has the same mass and the same speed but it's moving in the opposite direction. What that means is that before the collision, the momenta will have the same magnitude but will be negatives of each other because they're in opposite directions. So momentum of car one equals the negative of the momentum of car two. So that means the total momentum before the collision is zero, total momentum of the system is zero, and then after the collision we'll assume that the cars stick together and so the momentum after -- the total momentum after and in after collision you usually write an apostrophe there, a prime -- is going to equal the mass of the first car plus the mass of the second car, but they're both the same so they don't need subscripts. We'll just call it m in which case it's really two m, multiplied by this speed that they have after the collision, all equals zero because the momentum after collision equals the total momentum initially which we already establish is zero. Well, so we have two m v prime equals zero in which case the speed will be zero. Oh yeah, we can't say what the force will be though on the passenger, all we can say is that the change of momentum will be the same as it was before when they hit the tree. But we can't say anything about the force because we don't know through what distance the passenger will be brought to a stop; whether they're going to hit an airbag in which case they will be brought to a stop in a large distance, in which case there is a small force; or whether they are going to be stopped immediately by you know, just the dashboard padding in which case they would experience a large force.
