Question
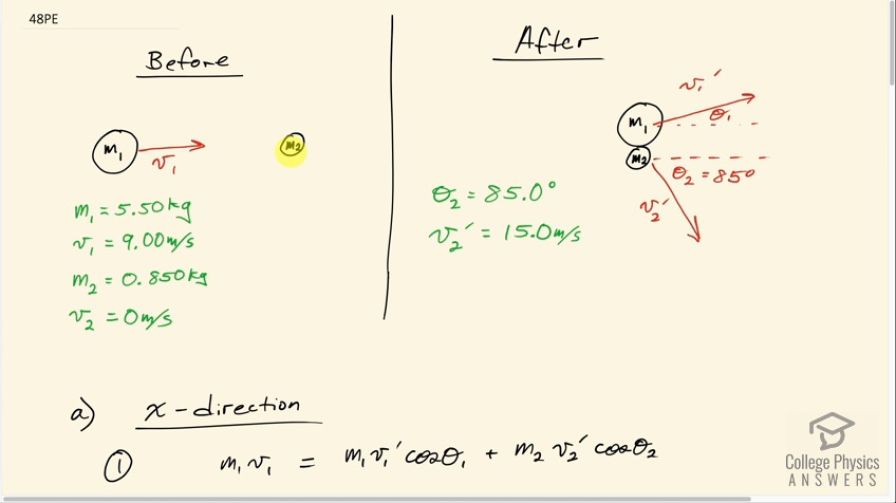
A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg bowling pin, which is scattered at an angle of to the initial direction of the bowling ball and with a speed of 15.0 m/s. (a) Calculate the final velocity (magnitude and direction) of the bowling ball. (b) Is the collision elastic? (c) Linear kinetic energy is greater after the collision. Discuss how spin on the ball might be converted to linear kinetic energy in the collision.
Final Answer
- The collision is not elastic.
- Immediately after collision the ball will be rotating such that a point on the edge of the ball will be moving faster than it's briefly arrested linear velocity. This will cause slipping that will linearly accelerate the ball, resulting in the conversion of rotational kinetic energy into linear kinetic energy.
Solution video
OpenStax College Physics, Chapter 8, Problem 48 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
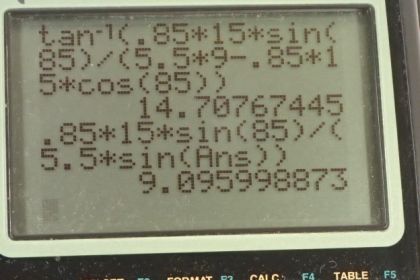
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A bowling ball with mass 5.50 kilograms is incident on this, initially at rest, pin which we'll call m 2 with a velocity of 9.00 meters per second. We'll setup our coordinate system so that the x-axis is along the initial velocity direction and the y-axis will be upwards perpendicular to that. And after the collision, we are told that the pin has a velocity of 15.0 meters per second at an angle of 85 degrees with respect to the initial direction of velocity of the ball so it's 85 degrees below horizontal in this picture. And our ball then is going to have a velocity that is gonna be to some extent at an angle Θ 1 above the horizontal in order for the momenta in the y-direction to equal zero in the end because that's what we had initially for the y-momentum. And then in the x-direction of course, the x-component of the momentum of the ball and the pin will equal the initial momentum of the ball. Okay! So we have to find v 1 prime and Θ 1. So for the x-direction, we have the initial total momentum is just that of the ball, m 1v 1, and after collision, the total momentum is gonna be m 1v 1 prime times cosine of Θ 1 because we are finding the adjacent leg; if this vector was the momentum vector which is gonna be you know, in the same direction as the velocity vector then this would be the adjacent leg of that momentum and so we use cos Θ 1 to find that and then add to that m 2v 2 prime times cos Θ 2. And there's nothing more we can do with this equation because we don't know v 1 prime and we also don't know Θ 1. So when you have an equation with two things unknown that means you need to have another equation involving at least one of those factors in order to solve for them. So when you have two unknowns, you need to have two equations so that means we have to look at the y-direction. So we have that the total y-momentum initially, which is zero, equals the y-momentum after collision, m 1v 1 prime times sin Θ 1— that's this vertically upwards component to the momentum of the ball and then minus and I put a minus there because the y-momentum of the pin is directed downwards in the negative direction so that's directed down here... this is m 2v 2 prime sin Θ 2 is this part here and then we have to do some algebra to solve for the unknowns. So I am going to rearrange equation number 2 and equation number 1 such that we have a single term on the left side containing the Θ 1 factor. So equation 2 version b is gonna be m 1v 1 prime sin Θ 1 equals m 2v 2 prime sin Θ 2 so you can say that I added m 2v 2 prime sin Θ 2 to both sides and then switched the sides around and the reason for doing this is because when we have two equations and the left sides are just a single term, we can then divide these equations and these factors are gonna cancel— the m 1's will cancel, the v 1 prime's will cancel— and then we'll be left with sin Θ 1 divided by cos Θ 1 which there is a trigonometric identity for and we can call that tangent Θ 1 and that will be the only unknown and we'll have tan Θ equal some stuff and then we'll take the inverse tangent of both sides to solve for Θ 1. Okay! But one thing at a time: let's rearrange equation 1 version b and we'll call this m 1v 1 prime cos Θ 1 equals m 1v 1 minus m 2v 2 prime cos Θ 2 so I subtracted m 2v 2 prime cos Θ 2 from both sides and then switched the sides around as well. Then we take equation 2 version b and divide it by equation 1 version b so that's m 1v 1 prime sin Θ 1 divided by m 1v 1 prime cos Θ 1 and that equals the right hand sides divided so that's m 2v 2 prime sin Θ 2 all over m 1v 1 minus m 2v 2 prime cos Θ 2. And these factors cancel and sin Θ 1 over cos Θ 1 can be substituted with tan Θ 1 and then the right hand side is unchanged here and then we'll take the inverse tangent of both sides to solve for Θ 1. So Θ 1 is the inverse tangent of m 2v 2 prime sin Θ 2 over m 1v 1 minus m 2v 2 prime cos Θ 2. So that's the inverse tangent of 0.850 kilograms—mass of the pin— times 15.0 meters per second— velocity after collision— times sin 85.0 degrees divided by 5.50 kilograms—mass of the ball— multiplied by its initial velocity of 9.00 meters per second minus 0.850 kilograms times 15.0 times cos 85.0 degrees and that gives 14.7 degrees is this angle above horizontal for the ball after the collision. Now that we know that angle, we can then figure out what the speed of the ball is v 1 prime by rearranging equation 2 and we'll call it version c and then dividing both sides by m 1 sin Θ 1 and so we have v 1 prime then is m 2v 2 prime sin Θ 2 over m 1 sin Θ 1. So that's 0.850 kilograms times 15.0 meters per second times sin 85.0 degrees divided by 5.50 kilograms times sin of 14.7077 degrees— that we found just now— and that's 9.10 meters per second. So our final answer for the velocity of the ball after the collision then, v 1 prime, is 9.10 meters per second, 14.7 degrees above horizontal. Part (b) asks us is this collision elastic? Well to answer that, we need to figure out the total kinetic energy before collision and after collision and compare them and if the kinetic energies are the same then we'll say: yeah, the collision was elastic. So initially the only kinetic energy is that of the ball and that's one-half 5.50 kilograms times 9.00 meters per second squared which is 223 joules. And after the collision, we have one-half times 5.50 kilograms times 9.10 meters per second squared plus one-half times 0.850 kilograms— mass of the pin— times its speed of 15.0 meters per second squared giving us 323 joules; this is definitely not the same number and so the final kinetic energy does not equal the initial kinetic energy and therefore the collision is not elastic. In part (c), we are meant to notice that this final speed of the ball— 9.10 meters per second— is greater than its initial speed of 9.00 which is a bit strange resulting from conversion of rotational kinetic energy into linear kinetic energy So immediately after collision this ball which, you know, has been rotating as it's been going down the bowling lane; its speed of rotation is not going to be changed by the impact because the impact is very instantaneous, let's say, so its linear velocity will be reduced a little bit by the collision but its rotational velocity will be unchanged and so that means its rotational velocity is going to be causing a point on the surface of the ball to be moving at faster than the ball's linear velocity and so it's going to be slipping, in other words. So this is gonna be spinning faster than it's supposed to. And that slipping is gonna cause a kinetic friction force here which will be opposing the slip and this friction force, we can see is pointing in the same direction as the linear velocity and is therefore going to accelerate it, the linear velocity, and it's also going to reduce the speed of the rotational velocity. And so we have this speed here v it's a little bit less than ω times r— ω being the rotational velocity and r being the radius— and this product is the tangental velocity of a point on the edge of the ball but the ball's linear velocity is gonna be a little bit less than that because of the collision that it just had and so therefore we had this slipping and this force is... since it's going to be increasing v and decreasing ω, it will do that until this equality is true and it's going to cause v to increase meaning that this rotational kinetic energy is being converted into linear kinetic energy.