Question
A 0.450-kg hammer is moving horizontally at 7.00 m/s when it strikes a nail and comes to rest after driving the nail 1.00 cm into a board. (a) Calculate the duration of the impact. (b) What was the average force exerted on the nail?
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 18 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
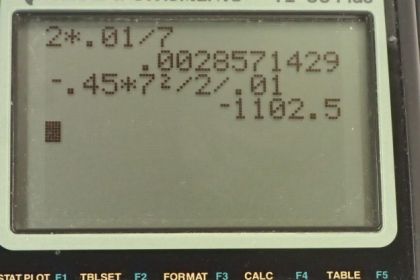
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 0.450 kilogram hammer is hitting a nail and the hammer initially moves with a velocity of 7.00 meters per second— it's going to the right— and it will hit the nail and insert the nail into the wood 1 centimeter and we convert that into meters by multiplying by 1 meter for every 100 centimeters so that's 0.0100 meters. And the final velocity of the hammer, we assume, is 0 meters per second. So the final velocity is labeled v prime, the initial velocity is labeled just v and in part (a), we are asked to figure out for how long is the hammer in contact with the nail? So the distance that the nail goes is going to be, or the hammer for that matter, will be the average velocity of the hammer multiplied by the time and the average velocity is the initial plus final velocities divided by 2 and this is a formula that's true when you have constant acceleration which we are gonna assume is the case here and then we'll solve this for t. So we'll multiply both sides by 2 over this sum of initial and final velocities... 2 over initial plus final. Okay! So we have then that t equals 2d over initial plus final velocity. So that's 2 times 0.0100 meters divided by 7 plus 0 which is 2.86 times 10 to the minus 3 seconds. So for 2.86 milliseconds, the hammer is pushing on the nail. In part (b), we are asked what is the force on the hammer or on the nail? I mean they are of equal magnitude, just opposite directions— those are Newton's third law pairs. So let's figure out the force on the hammer and I guess strictly speaking, if we are looking for the force on the nail, this is the net force on the hammer... the force on the nail will be the opposite of the force on the hammer so that's gonna be the opposite of 1100 newtons; I'll get to why this is so in a second. Okay! But first, impulse is net force multiplied by time and then we can solve for net force by dividing both sides by t. And there is only one force on this hammer which is the force exerted by the nails— this is the force on the hammer due to the nail— and so since that's the only horizontal force that makes it the net force. And so we have that the net force then is the impulse divided by time and time is 2d over v plus v prime and so if we are going to divide by this time, we can instead multiply by the reciprocal of this fraction which is where I get this ΔP times v plus v prime over 2d... this is a plus here. Okay! And then I substituted for ΔP and wrote it as final momentum—mass times final velocity— minus initial momentum which is mv and then this is copied here. And the final velocity is zero so this term is zero and this term here is zero so we are left with negative m times v times v so that's v squared over 2d— this is our net force on the hammer. So that's negative of 0.450 kilograms times 7.00 meters per second squared divided by 2 times 0.0100 meters which is negative 1100 newtons. Now the question, strictly speaking, was asking for the force on the nail? So the force on the nail due to the hammer is the opposite of the force on the hammer due to the nail so that's negative of negative 1100 newtons, or in other words, positive 1100 newtons is the force on the nail due to the hammer.