Question
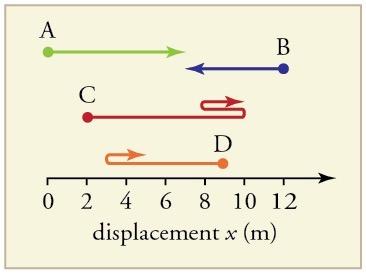
Find the following for path C in Figure 2.59: (a) The distance traveled. (b) The magnitude of the displacement from start to finish. (c) The displacement from start to finish.
Final Answer
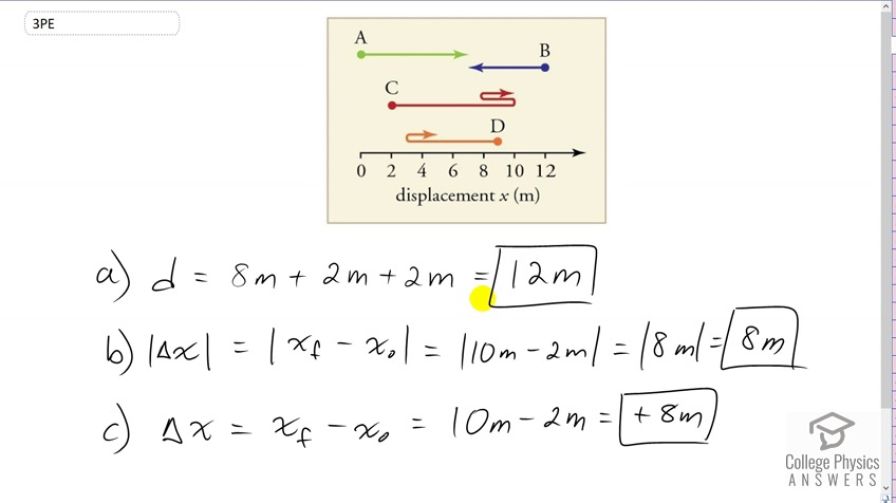
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 2, Problem 3 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko In this question, we consider the path labeled letter C. And they ask, ‘What is the distance traveled?’ in part A, ‘What is the magnitude of the displacement?’ in part B and ‘What is the displacement?’. And so, they get a little bit tricky because they have some backtracking that happens here, and that backtracking has no effect on the displacement, but it does change the distance traveled. So, the person walking goes from a position of 2 meters all the way to position of 10 meters and then goes back 2 meters to the 8 metre mark and then proceeds forward again to the 10 metre mark. And so, the distance traveled is going to be from 2 to 10, which is 8 meters. And then, the next segment of their path takes them from 10 back to 8, which is a distance of 2 meters. And then, from position 8 back to position 10 again is another 2 meters for a total of 12 meters is the distance traveled. Now, to find the magnitude of the displacement, we… I wrote these absolute value signs here, which means we take the positive of whatever number we end up with between these bars. And, the displacement is the final position minus the initial position. And the final position is 10. The initial position is 2. And so, the magnitude of that displacement is 8 meters. And the displacement is all of that again, but without the absolute value signs. And so, in this case, that will give us the same answer as the magnitude of the displacement. But, had the person been starting on the right hand side and proceeded to the left, we would have got a negative displacement. But, in this case, we have a positive displacement. So, we have final position minus the initial position. 10 meters minus 2 meters and we have positive 8 meters. And we put a plus sign there to emphasize that this is a vector and that it has a direction and the direction is in the positive direction 8 meters.

