Question
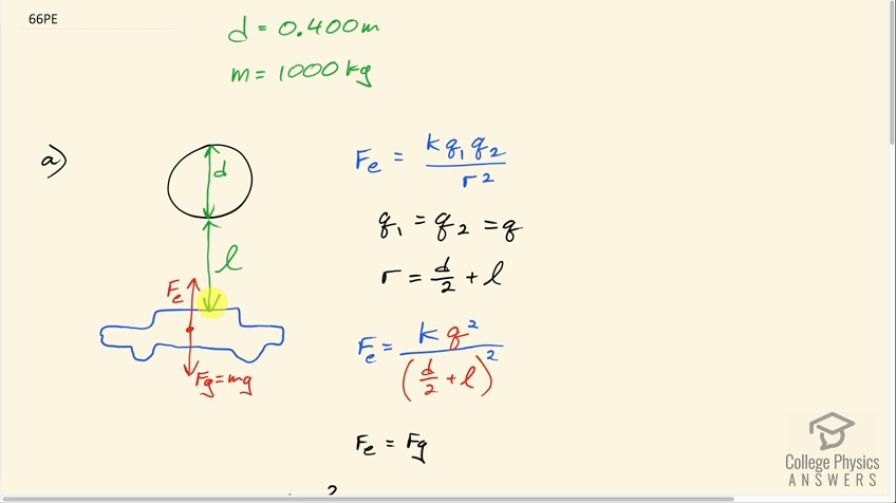
A wrecking yard inventor wants to pick up cars by charging a 0.400 m diameter ball and inducing an equal and opposite charge on the car. If a car has a 1000 kg mass and the ball is to be able to lift it from a distance of 1.00 m: (a) What minimum charge must be used? (b) What is the electric field near the surface of the ball? (c) Why are these results unreasonable? (d) Which premise or assumption is responsible?
Final Answer
- This field strength is two orders of magnitude greater than that needed for dielectric breakdown of air (). This field strength can not exist in air without causing sparks.
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 66 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
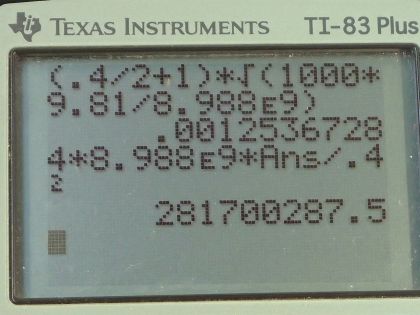
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A wrecking yard inventor wants to charge up a ball of diameter 0.400 meters to lift a car which is of mass 1000 kilograms and that car will have the equal but opposite charge as the ball does. So I make the assumption that this ball is a conducting sphere— it's made out of metal— in which case it can be modeled as a point charge with a point at the center of the ball and so the total distance between the car and the ball is this half diameter plus the distance from the ball to the car. So for part (a), we are gonna say that the force due to the charge is going to equal the gravity because that's the point at which you can start to lift the cars when these two are equal. And the force is kq 1q 2 over the total distance from the car to the center of the ball squared and q 1 and q 2 are the same and so we'll just call it q and this distance r is half the diameter plus the distance from the ball to the car, which we'll call l. So we substitute for q 1 and q 2 both with q in which case we have q squared and divide that by this distance, r, diameter of the ball divided by 2 plus the distance from the ball surface to the car squared. And this electrostatic force has to equal gravity so we can equate this with mg and then solve for the charge q. So first we'll solve for q squared by multiplying both sides by d over 2 plus l squared over k and then we have q squared is mg times d over 2 plus l squared over k and then take the square root of both sides to solve for q so q then is d over 2 plus l times the square root of mg over k. So that's 0.400 meters—diameter of the ball—divided by 2 plus 1.00 meter from the ball to the car because we are told that l is 1.00 meter by the way so the ball is meant to be 1.00 meter above the car and multiply that by square root of 1000 kilograms—mass of the car— times 9.81 newtons per kilogram divided by Coulomb's constant and that gives 1.25 times 10 to the minus 3 coulombs is the charge needed on both the ball and the car of opposite signs. So the electric field on the surface of the ball then is going to be Coulomb's constant times this charge we found in part (a) divided by the radius of the ball squared and the radius is half the diameter so we end up with 4kq over diameter squared. So that's 4.00 times Coulomb's constant times 1.2537 times 10 to the minus 3 coulombs divided by 0.400 meter squared which is 2.82 times 10 to the 8 newtons per coulomb. Now this field strength is two orders of magnitude greater than what's needed for dielectric breakdown of air. So when there's an electric field that's too strong in air, it causes the air to be ionized... it separates the electrons from their atoms and so you have free electrons going around which causes the air to be conducting and when it's conducting, it will have sparks and so electric field's greater than 3 times 10 to the 6 newtons per coulomb cannot exist in air because they cause sparks and those sparks cause charge transfer which therefore reduces the electric field that the charge distribution that was originally present created. Okay! So it's unreasonable to use static charge to lift heavy objects because in all other respects, the numbers here are reasonable: the mass of a car is about a 1000 kilograms; this distance of 1.00 meter is a reasonable expectation for being able to lift a car; and so the only thing you can't really do then is use this technique at all since you will need such a big charge on these two objects that you will have sparks all the time and which will thereby reduce the charge difference.