Question
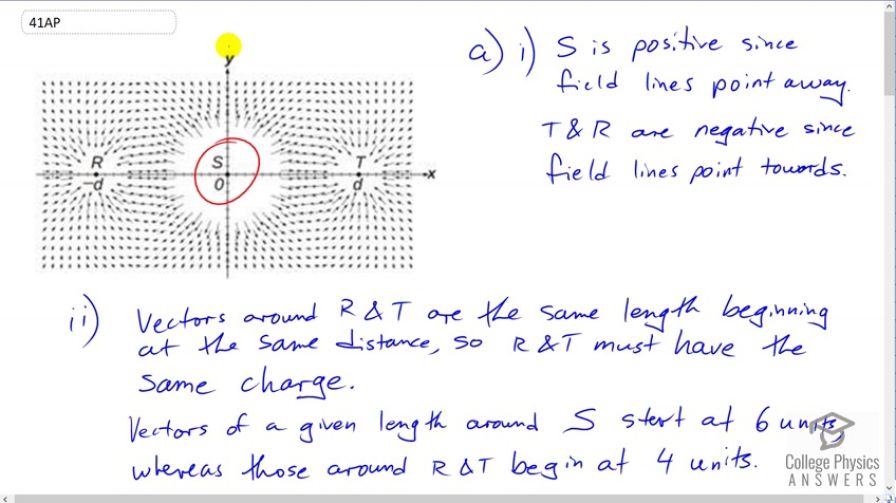
Figure 18.67 below represents the electric field in the vicinity of three small charged objects, R, S, and T. The objects have charges −q, +2q, and −q, respectively, and are located on the x-axis at −d, 0, and d. Field vectors of very large magnitude are omitted for clarity.
-
- Briefly describe the characteristics of the field diagram that indicate that the sign of the charges of objects R and T is negative and that the sign of the charge of object S is positive.
- Briefly describe the characteristics of the field diagram that indicate that the magnitudes of the charges of objects R and T are equal and that the magnitude of the charge of object S is about twice that of objects R and T.
- On the axes below in Figure 18.68, sketch a graph of the electric field E along the x-axis as a function of position x.
- Write an expression for the electric field E along the x-axis as a function of position x in the region between objects S and T in terms of q, d, and fundamental constants, as appropriate.
- Your classmate tells you there is a point between S and T where the electric field is zero. Determine whether this statement is true, and explain your reasoning using two of the representations from parts (a), (b), or (c).
Final Answer
- i) S is positive since field lines point away. T&R are negative since field lines point towards them.
ii) Vecgtors around R & T are the same length beginning at the same distance, so R&T must have the same charge. Vectors of a given length around S start at 6 units away, whereas those of the same length around R&T begin at 4 units away. See video solution for why this means S has twice the charge magnitude of R&T. - See video for graph.
- No, this is not possible since vectors are always pointing to the right, and because the equation for the net electric field in this region will always be positive. See the solution video for an explanation as to why the equation is always positive.
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 41 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We're shown a vector field for the electric field around three different charges. The charge in the middle is plus two q and the charges at positions d and negative d on the x axis are negative q and negative q. So part A part one asks us to use this vector field to confirm that the charge at s is positive and charges t and r, negative. We can tell that's true because the field lines point away from charge s. Field lines always point in the direction of the force that would be applied on a positive test charge. So if you put a positive charge here, this field line indicates it would be repelled from this charge. The only way that's possible is if this charge at s is positive as well. For charges t and r the field lines are pointing towards charge t and charge r and that means a positive test charge placed here would be attracted to the charge here. That must mean that the charge is negative at t and at r. Okay. Then the next question is, confirm that charges r and t are equal and that charge s is two times in magnitude the charges r and t. Well, r and t are equal because the field lines are about the same length at the same distance from the charges r and charge t. If you go about one, two, three, four units away, four units of distance away from charge t to get to the tail of a vector, the tail is where it begins, it'll have a certain length. You go four units away from charge r and you'll get a vector beginning there of about the same length at the same distance. So that means r and t must be the same charge. Now for the charges -- for the field lines around charge s, it looks like you have to go about one, two, three, four, five, six units away to get to the tail of a vector which is the same length as a vector only four units away around charge t or r. So, what that means is if you write down the formula for the electric field due to charge s, it's going to be k times Q s over distance r s squared. We found that distance is about six and I don't write any units there because we don't know what the units are. But knowing the important thing is that they are the same in both equations here. So we have Q s times k over 36 is the electric field around charge s and the same electric field around charge r, and I say the same because the length of the vector represents the magnitude of the field. The length of this vector is the same as the length of this vector. So the E s and E r equal, in magnitude anyhow. For E r we have k charge r divided by the distance from r squared, that's about four units, so that's k Q r over 16. So we equate these two here and then multiply both sides by 36 over Q r and also divide both sides by k. You end up with Q s over Q r equals 36 over 16 which is approximately two. If this was 32 then it would be exactly two. But we're just eyeballing this sort of sketch here so you can't expect to have precision here. So two is the factor by which Q s and Q r are different. The next part of this question asks us to graph the electric field along the x axis. So we're given these axes here with d and negative d labeled on them and these are going to be asymptotes. When -- let's look at this picture down here -- when -- we can even move this up here, get a little bit closer. When we're at a position here to the left of charge r, the electric field is pointing to the right and so it is positive. As you get closer and closer to r, it's going to become more and more positive. As r decreases, this electric field increases. So as r gets smaller, this fraction will get bigger to the point where as r approaches zero, this fraction approaches infinity and it's going to be positive infinity in this case. So we have this picture here where this negative d is an asymptote and it gets ever and ever closer to it, but never quite touches it. Okay. Then on the other side of charge r, the field is pointing to the left and so it is negative. When it is close to ror when it's almost negative d, it's going to be very largely negative. So it's an asymptote down this direction. Then as it goes between r and s it's going to be of this, whatever the length of these vectors are, that's the magnitude that it is negative, until it starts to get close to charge s at which point it will become very, very, very negative and then this position at the origin where charge s is, is also an asymptote. Then on the other side of s the direction changes and just beside s on the right hand side, it is very largely positive, pointing to the right. So again it's an asymptote and now it's up here and it goes down to this level here between s and t. Then once you get close to t, it's going to be very largely to the right again because t is negative and it's attracting this -- it's making these field lines go towards it. Okay. Then on the other side of t it's really negative because it's pointing to the left and then it gets less and less negative as you go further away from t. So this is a sketch, I mean it's sort of a rough drawing. This distance here should be greater than this distance here but you know, that's a very fairly minor point and it would be difficult to really indicate that in your sketch. This should be a greater distance here just because s is a greater magnitude charge than t is. All right. Then, in part C we're asked to find a formula for the field between s and t. So the electric field is going to be the magnitude of the filed due to s nd that's going to be positive because that'll be to the right, and then we're going to have minus the magnitude of the field due to charge r. This charge r is going to have an electric field pointing to the left in this region between s and t and so it is negative. Then add to that the electric field due to t which is pointing to the right towards t and so it's positive. Then as we substitute in charges here, I'm just not bothering to write it because it's just too much work to write, but you can imagine that there are absolute value signs around all of these charges. We've taken care of direction already in our analysis here and now it's just magnitudes of the charges that we substitute in. So the electric field due to charge s is Coulomb's constant times two q divided by xsquared, x being the distance to the right from the origin, let's say here for example, and then minus from that k q over x plus d squared because the distance from charge r is going to be x plus an additional distance d, so the total distance being x plus d, and then add to that the field due to charge t which is going to be k q over d minus x squared. So, the distance between here and here, this point of interest and t is going to be the full separation from t to the origin which is d, and then minus the amount by which it's away from the origin x. So we have d minus x squared. You can factor out the k q just to make it look a little nicer and you get k q times two over x squared minus one over x plus d squared, plus one over d minus x squared. That is the net electric field between charge s and t. Then a student says well, there's a point between s and t where the field is zero, so says the student. This is not possible and there are two good reasons for that. One, we can look at this picture and see that the vectors are always pointing to the right and there is no point where they will look like they'll become shorter and zero and so this indicates from this vector field that the field cannot be zero. We can also look at this formula and this is the net electric field that we calculated -- or we didn't calculate it. We determined this equation in part C and we'll see that this is always going to be positive. That's because x plus d squared is always going to be greater than d minus x squared because this is taking the sum of two numbers and this is taking their difference and since we're squaring, it doesn't matter if the difference is negative or positive. The difference is always going to be of smaller magnitude than the sum. So this sum squared is going to be greater than this difference squared. So that means this fraction is always going to have a smaller magnitude than this fraction since the denominator has a greater magnitude. So if we're dividing by a big number we're going to get a small fraction. What that means is that well, since this fraction gets a negative in front of it and this fraction has a positive in front of it, given that this has the bigger magnitude than this one, this difference is always going to be greater than one. With that difference being greater than one, so this part is going to be greater than one, there's no other way for this thing to become zero or negative or anything like that. It's always going to be a positive number because this is a constant that is going to be positive because x is positive to the right of point s. These things are positive, we're always using magnitudes of charge here and so this electric field then is going to be positive. Q.E.D. Quod Erat Demontrandum, that's the Latin for "All done. We have shown what was meant to be shown."