OpenStax College Physics for AP® Courses, Chapter 18, Problem 16 (Problems & Exercises)

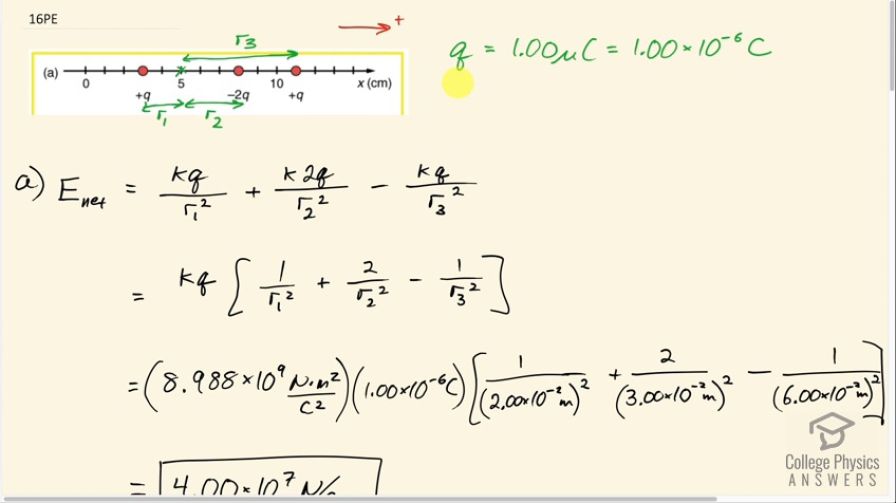
This is College Physics Answers with Shaun Dychko. We have a lot of questions to answer in number 16 here, let's start with part (a) which asks what is the electric field at x equals 5 centimeters given that q is 1.00 microcoulomb which is 1.00 times 10 to the minus 6 coulombs. So we have a charge of positive q here at position x equals 3 and it's some distance we will call r 1 from the point of interest at x equals 5 and then there's this charge negative 2q at this position which is this distance r 2 from the point of interest and then there's this charge plus q at this distance r 3 from the point of interest. So the net electric field will be the sum of all the fields from each of these charges but it's the vector sum which is to say that we need to pay attention to the direction of the electric field from each of these charges and we are gonna take to the right to be the positive direction. This charge—plus q—here will exert a force to the right on a hypothetical test charge that was placed here and so that means its electric field would be to the right. This charge—negative 2q—will also exert a force to the right because it will be attracting a positive test charge placed here and this charge here will be exerting a force to the left on a positive test charge here and so its electric field would be to the left and so the field due to this charge will be in the negative direction and so there's terms here for each of those. And so this is the term for this charge here, a distance r 1 from x equals 5 and so its electric field will be positive because it will be to the right— kq over r 1 squared— and here's the term for the field due to this negative 2q charge and I am just... the only positive or the negative we need to be concerned with the one that reflects the direction of the field due to this charge and it would exert a force to the right, which is the positive direction so I am putting positive k2q over r 2 squared. And then this charge will exert a field to the left and so it's a minus kq over r 3 squared. The kq can be factored out from each of these terms so we have kq or times 1 over r 1 squared plus 2 over r 2 squared minus 1 over r 3 squared and then we plug in numbers to get our answer. So this is 8.988 times 10 to the 9 newton meters squared per coulomb squared— that's Coulomb's constant— times the charge of 1.00 microcoulomb times 1 over 2.00 centimeters squared but I write centimeters as times 10 to the minus 2 meters because there are two tick marks on this centimeter scale between this charge and x equals 5 and then plus 2 over 3.00 times 10 to the minus 2 meters squared— that's the distance from this negative 2q charge to x equals 5— so that's r 2, in other words, is of magnitude 3.00 times 10 to the minus 2 meters, we square that and then minus 1 over 6.00 times 10 to the minus 2 meters squared— the distance from here to x equals 5— and that works out to 4.00 times 10 to the 7 newtons per coulomb and that's positive which is to say it's to the right. Okay! Part (b) asks at what position between 3 and 8 is the total electric field the same as that for this charge by itself? And so we are searching for a position where the electric field due to this positive q charge here and this positive q charge on the right hand side, at what position do the fields from each of these charges make zero? And so we are looking for a position that is equidistant from these two charges so the midpoint between them is where the electric field's will be zero due to those exterior charges and therefore we will be left only with electric field due to negative 2q as though it was alone. And so here we have a distance of one, two, three, four, five, six, seven, eight units between these charges and so at this position—four units, from each of them—that's where the electric field due to the exterior charges will add up to zero because this one will be exerting a field to the right and this right hand charge will be exerting a field to the left of equal magnitude because they are equal magnitude charges and this point is equidistant from each of the charges and so here is the point that will answer our question and that's x equals 7. Okay! So part (c) asks can the electric field be zero anywhere between 0 and 8 centimeters? Let's copy this picture down below because it is getting a bit messy up there, let's put it down here say. So between 0 and 8 is what we are interested in. Now if we look at between 3 and 8, clearly there will be no point where the electric field is zero because both of these charges are exerting fields in the same direction and this charge is pointing to the left but this charge will be having a field to the right with greater magnitude for two reasons: one that this point is closer to this charge and furthermore, this charge is greater magnitude than this one so this is a charge that we can basically ignore for this part of the question. And then this one will be exerting a field to the right and this exerts a field to the right as well and so regardless of where we are between these two charges. the net field will be to the right, there will be no point where it's zero. However, on the left side of this charge, it turns out that the answer is no, there's no point where it is zero but it is worth examining because at any point here between 0 and 3, we have this charge exerting a field to the left and then this charge is exerting a field to the right and so it's plausible that there will be some point where these are of equal magnitudes in opposite directions making a net field of zero and because, you know, even though this charge is small in magnitude than this one but the point is that it's closer to this and so maybe that compensates for its smaller charge and these can be equal but let's see. So the net field is gonna be negative kq over r 1 squared— that's the distance from this first charge to the point of interest— and it's negative because it's exerting a field to the left because it's a positive charge and it would exert a force on a positive test charge placed here to the left and then we have plus k2q over r 2 squared— r 2 being the distance from here to this charge— and that field will be to the right because it's a negative charge which would attract a positive test charge placed here and then negative kq over r 3 squared is the field due to this charge and this one would repel a positive test charge here towards the left so that's why there's a minus here. Okay! And we can substitute for r 2 and r 3 and express them in terms of r 1 so r 2 is r 1 plus 5.00 additional centimeters and then r 3 is r 1 plus an additional 8.00 centimeters— that's the separation between this charge and this one here— so we can substitute that in place of r 2 and r 3. And supposing this equals zero, we can divide both sides by kq and zero divided by kq is still zero and we are left with negative 1 over r 1 squared plus 2 over r 1 plus 5.00 centimeters squared minus 1 over r 1 plus 8.00 centimeters squared equals zero. So then we have to try to solve this equation; now solving it analytically, which is to say, you know, find a common denominator and then add these or subtract these fractions and then solve for the unknown would be very tedious because we would have r 1 squared multiplied by r 1 plus 5.00 squared multiplied by r 1 plus 8.00 squared that would be our common denominator and so then in the numerator here, we would be multiplying all of those binomials which would make a r 1 to the power of 6 it would be a polynomial with r 1 to the power of 6 in it and that would be really hard to solve so we use a graph. So this is the distance from this charge on the left side so this is the distance from this positive qr 1 in other words and this is... this formula here, this one, written as a spreadsheet formula— I am using Google Sheets here and so we have negative 1 over A2 represents r 1 squared plus 2 over r 1 plus 5 squared minus 1 over r 1 plus 8 squared and the units for this r 1 is centimeters. I didn't put units for the electric field because the units are gonna be strange since I am using a denominator with centimeter squared instead of meters squared but there's no need to change it to meters squared since we are looking for... we don't really care what the units of the electric field are, we just care whether it's zero. Okay! So here's a graph of the net electric field based on how far to the left we are from this leftmost charge here and of course it's a very strong field, strongly negative when we are close to this leftmost charge where we are only 0.1 centimeters away from it and then it goes towards zero the further away we get from the leftmost charge and we can see that it's approaching zero but it never quite reaches zero, it just gets smaller and smaller in magnitude the further we go and for these distances here, we need even more precision to even see the difference but... yeah, so. Anyway this is to say certainly between so now once we are at distance of 3.0 centimeters away from this charge, we have already got x equals 0 when we are 3.0 centimeters away from this charge and the question asks is there any point between 0 and 3 where the field is zero? And the answer is no because we are still at negative 0.088 for this field here. So there we go; the answer is no, the electric field does not become zero between 0 and 8. Okay! Then in part (d), at large distances, the electric field approaches that of a point net charge and so the question is consider scenario (a) and consider scenario (b) and the electric field approaches zero at infinity for each of these but in which scenario—(a) or (b)— does that happen more quickly? Now since the electric field approaches that of a point net charge, it will approach zero more quickly for scenario (a) since the net charge would be zero far away from it because we have a negative 2q in the middle and then a positive q here and then a positive q here which makes a positive charge of zero. Whereas for scenario (b), there's a positive 4q in the middle and then a negative 3q in total in the exterior which makes a net charge of plus q and so this field would, at large distances, would be k single q over whatever that large distance is squared and that will approach zero but it will approach zero slowly whereas this one will approach zero more quickly since the net charge is zero. So part (a), it approaches zero more quickly. Okay! And then finally question (e): at what position to the right of 11.0 centimeters is the total electric field zero besides looking at infinity? Alright! So the charge is 1.00 microcoulomb for q and we are going to the right of this right-hand charge here and we have these distances— r 1 from this first charge; r 2 from this second charge; and r 3 from this third charge. The field due to this charge here on the left side will be positive to the right of magnitude kq over r 1 squared, this field due to this middle charge will be negative because it will be to the left because it would attract a positive test charge placed here and so that's negative k2q over r 2 squared and then this charge would exert a field to the right kq over r 3 squared. We can express r 1 and r 2 in terms of r 3 suppose so r 1 is r 3 plus 8.00 centimeters because whatever the distance is from here to the point of interest plus the separation between these two charges, which is 8.00 centimeters, and then r 2 is r 3 plus 3.00 centimeters and we substitute that in for r 1 and r 2. And then we want to know where this field is zero so we divide both sides by kq and the right-hand side still says zero and on the left-hand side, we have 1 over r 3 plus 8.00 centimeters squared minus 2 over r 3 plus 3.00 centimeters squared plus 1 over r 3 squared. So we need to use a graphing calculator or a spreadsheet to answer this question because this is a very... you know, just as for the question before, part (b), this would be a polynomial of degree 6 so it would be difficult to solve analytically so we can look at this thing here. This is the distance from the right-hand charge and this is the electric field and I have substituted this is the spreadsheet version of all of this and we are looking at the field for different distances from the right-hand charge—that distance is r 3— and I am going by increments of half a centimeter and we are seeing that it starts off as a big positive number and then becomes smaller and smaller positive... smaller positive and so on and so on until finally when we are 19.5 centimeters away from the right-hand charge, the field goes from positive to negative. Now in order to go from positive to negative that means it must have passed through zero at some point in here and so this is an interval in r 3 that we should plot with greater precision to figure out more precisely where this field is zero so that's what this second section is for. So I started at 19.5 and then went up by 0.01 centimeters in each row here and we can see that at about 19.60 and we can legitimately say 0.60 because we are using precision of the hundredths place here it's really close to zero here and you can get arbitrarily close to zero with your spreadsheet; you can plot to a thousandths place or the hundred-thousandths place and so on. And so we are gonna say that 19.60 is the distance from the right-hand charge where the electric field is zero. And so to answer the question with a value of x, we'll add 11.00 centimeters to that since this charge starts at 11.00 and so we have 11.00 plus 19.60 which is 30.60 centimeters is where the electric field is zero.